CONDOTTE DI AVVICINAMENTO E DISTRIBUZIONE

Acquedotto

L’acqua stoccata nei serbatoi va poi condotta alle singole utenze.
A tale compito sono demandate le reti di distribuzione, ma sovente occorre interporre tra serbatoio e rete di distribuzione vera e propria una condotta detta di avvicinamento.
Queste ultime di norma non dovrebbero fare servizio lungo il percorso, soprattutto quando la loro lunghezza é considerevole (a, per esempio, Pisa raggiungono i 6 Km). Ma, se distribuzione é necessaria lungo il loro percorso, questa deve essere affidata ad una apposita condotta.
La lunghezza della condotta di avvicinamento é stabilita, ovviamente, dalla posizione del serbatoio rispetto al centro cittadino e quindi in generale é funzione della conformazione morfologica locale in quanto, tendendo a realizzare serbatoi del tipo interrato o seminterrato, questi avranno ubicazione nelle alture circostanti il centro da servire.

Si suole distinguere le reti di distribuzioni in :

reti ad anello;
reti ad arteria principale;
reti aperte.
Le prime due rispondono a precise esigenze di buon funzionamento, la terza é tipica degli acquedotti rurali, delle distribuzione in case sparse ecc.. La condotta di avvicinamento, nel caso di retio ad arteria principale si confonde, sovente con la stessa arteria.
Nel paragrafo che segue si dettaglieranno gli schemi precedentemente elencati.
E’ ancora da precisare che la rete di distribuzione non alimenta direttamente le singole utenze, di norma si limita a trasportare e distribuire l’acqua lungo le strade cittadine. Dalla rete di distribuzione l’acqua viene poi prelevata dalle singole utenze con condotte di allacciamento che devono rispondere a requisiti tecnici e realizzativi diversi e diverso può essere il relativo stato giuridico.

Schemi di reti di distribuzione

La distribuzione ad anello

Esaminiamo dapprima la distribuzione ad anello, indubbiamente più classica e certamente la più ricorrente.
E’ lo schema naturale delle città a pianta più o meno circolare (Milano, Bologna, Pisa ecc…)
Dal serbatoio si diparte una condotta di avvicinamento che alimenta un anello principale.
Una regola un tempo seguita dagli acquedottisti era che l’anello principale dividesse in due la città lasciando al di fuori di esso eguale entità di popolazione di quella racchiusa all’ interno.

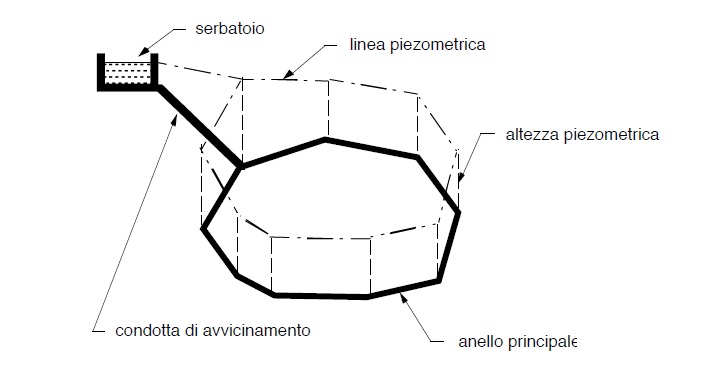
La figura che precede illustra un tale schema indicando anche la piosizione della linea piezometrica che sovrasta la condotta stessa e ne governa le leggi di flusso.
Di certo con l’estendersi delle città a macchia d’olio e con il progressivo “svuotamento” dei centri storici (che si é verificato negli anni “60 e “70) la regola di cui sopra anche se inizialmente rispettata é venuta a cadere.
Tra l’altro onde poter realizzare un anello principale é necessario che vi siano infrastrutture viarie o altri tipologie urbanistiche che permettano la realizzazione degli anelli.
All’ uopo vanno molto bene le circonvallazioni (vedi quelle di Milano od i viali di Bologna) o le linee delle vecchie mura cittadine (vedasi ad esempio Lucca, che ha tuttora le mura complete, o Pisa).
L’anello principale non fa, di norma erogazione lungo il percorso ma solo di trasporto e di riequilibrio delle pressioni.
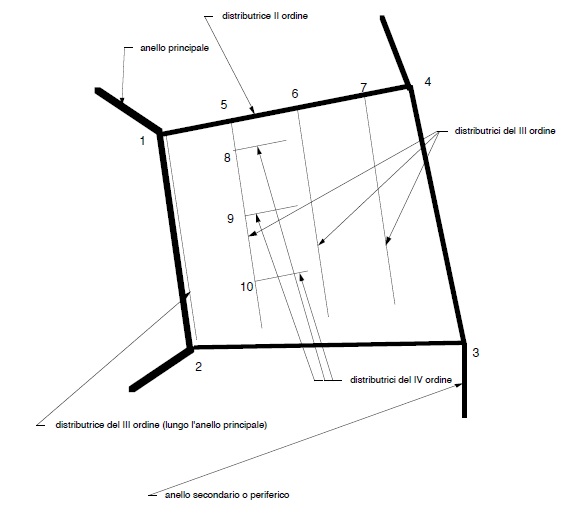
Da esso si dipartono, da punti detti nodi, le vere e proprie condotte di distribuzione così come indicato nella figura seguente.

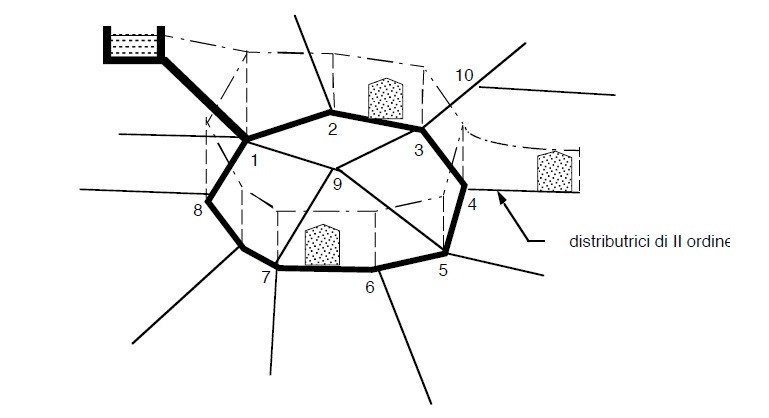
Le condotte distributrici verso il centro sovente si raccordano tra loro per assicurare un servizio migliore e per riequilibrare le pressioni. Il successivo espandersi delle città ha portato, successivamente alla realizzazione di anelli secondari che raccordavano le varie condotte che dalli nodi dell’anello principale distribuivano l’acqua in periferia.
Per tali motivi tali anelli hanno spesso preso il nome di anelli periferici.
La necessità di raccordare tra loro le distributrici del II ordine fu dettato e dalla opportunità di garantire un servizio in periferia nel caso di necessità di interruzione di qualche distributrice e soprattutto dalla necessità di riequilibrare le pressioni.

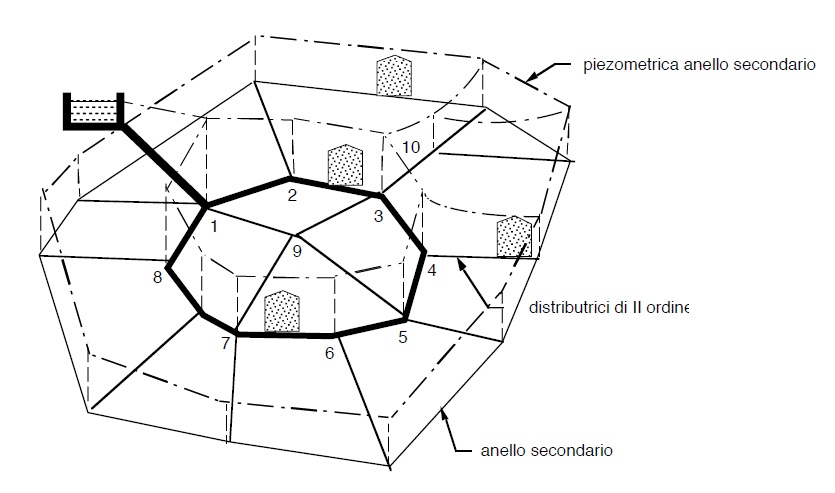
Ulteriori ampliamenti delle città verso l’esterno hanno portato a trasformare il primo (e poi successivamente gli altri) anelli periferici in anelli principali, con collegamenti diretti di questi alla condotta di avvicinamento e quindi , in generale con innalzamento delle piezometriche periferiche, come illustrato nel grafico che segue.

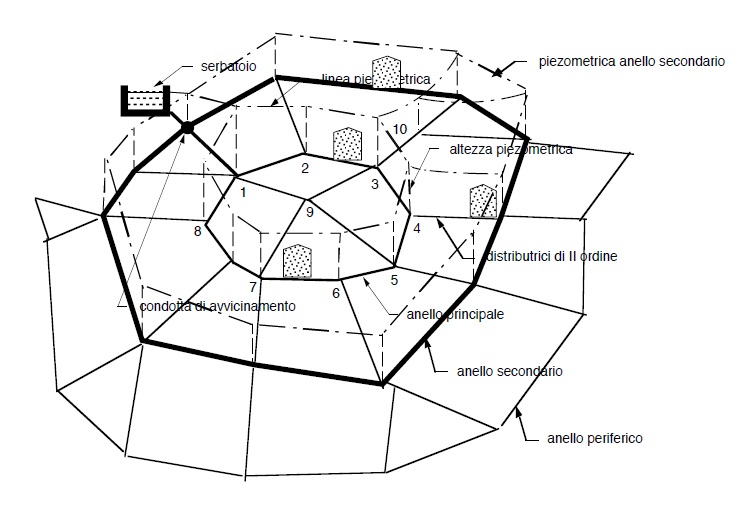
Conseguentemente, man mano che la città si espande verso l’esterno sirgono ulteriiri anelli periferici o quanto meno tratti di tali anelli.
Ma quanto sopra vali nelle grandi linee.
Occorre esaminare come impostare la distribuzione (vera e propria) tnel tratto di territorio compreso tra due distributrici del II ordine e due anelli contigui (ad esmpio tra il principale ed in secondario).
La figura che segue illustra una tale distribuzione.

Si noti che le maglie non sono spinte oltre il livello spra menzionato, ciò in quanto miglioramenti di servizio che vi potrebbero essere collegando ad entrambe le estremità le distributrici del III ordine si traducono anche in difficoltà di gestione in caso di interventi di manutenzione con necessità:

di operare su molte saracinesce per ottenerne il sezionamento;

di conoscenza di estremo dettaglio delle reti, conoscenza spesso solo tramandata oralmente;
maggiori costi di costruzione (necessità di ulteriori pozzetti, saracinesche ecc..

Dalla figura precedente si può notare come per assicurare la distribuzione lungo l’anello principale é stata indicata una distributrice del III ordine
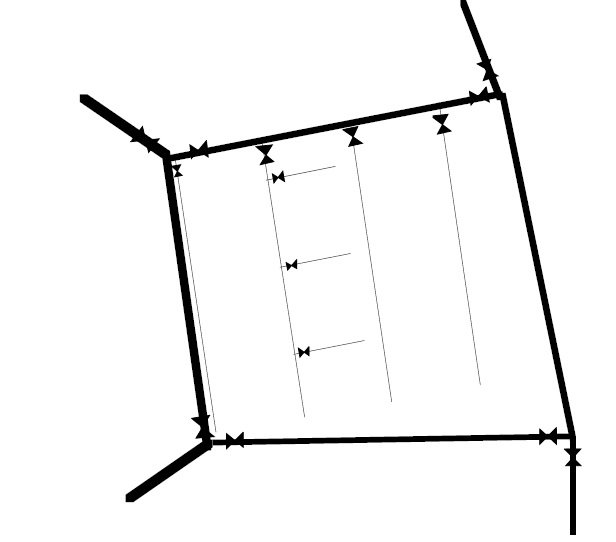
La figura che segue riprende lo stesso schema della precedente e lo completa con l’indicazione delle saracinesche. Da queste é evidente l’ampia possibilità di sezionare ed isolare i vari tronchi di condotta arrecando il minor pregiudizio possibile al servizio idrico.

La distribuzione ad arteria principale

Va sotto il nome di distribuzione ad arteria principale una serie di sistemi più o meno complessi di reti utilizzati in centri abitati che hanno in planimetria una direzione prevalente sulla seconda.
In genere a tale schema fanno riferimento le città costiere abruzzesi e marchigiane.
Queste si snodano tra due sistemi di colline l’uno a Sud, l’altro a Nord e sono attreversate dal corso d’acqua che ha modellato la vallata.
La figura che segue da una vista dal mare di un tale schema cittadino.

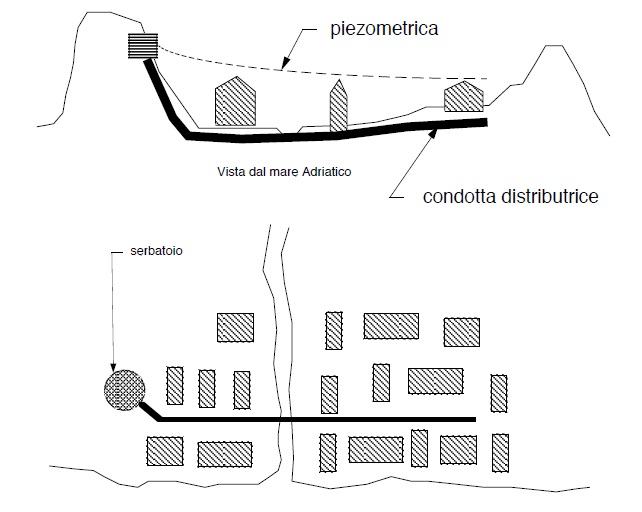
Il più semplice shema idraulico é quello della figura che precede. Su una delle colline si posiziona un serbatoio seminterrato e da questo si fa partire una rete distributrice lineare (arteria principale) che distribuisce l’acqua al centro abitato. E’ evidente anche dall’ esame grafico della menzionata figura come le ultime abitazioni siano svantaggiate ed abbiano problemi di rifornimento idrico in specie ai piani più alti.

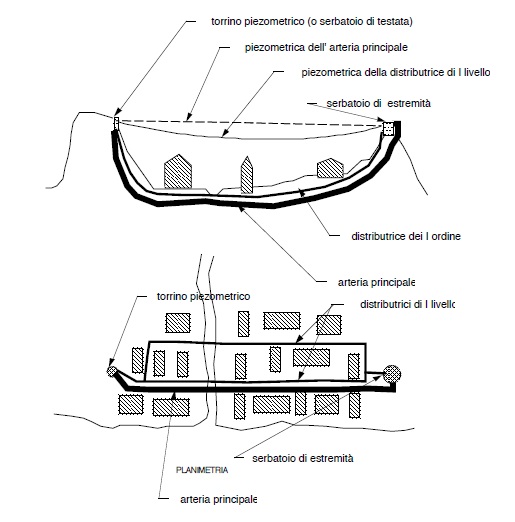
La figura che precede é invece relativa ad uno schema estremamente corretto ma anche molto costoso
Vengono realizzati due serbatoi, uno dei quali, il primo, può avere anche capacità modeste sino a ridursi ad una sola torre piezometrica.

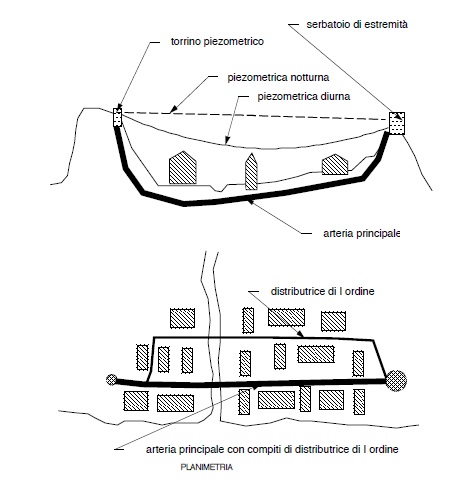
L’acqua perverrà dalla adduttrice al primo serbatoio (torrino) e da questo con una apposita condotta (arteria principale) al secondo. Da entrambi verrà inviata alla rete di distribuzione. Ne segue una piezometrica che avrà due punti fissi (le estremità ) ed il punto più basso sarà quello di equilibrio tra le acque provenienti dai due serbatoi.
Un tale schema é tuttavia molto costoso, pertanto si ricorre sovente a quello rappresentato nella figura che segue, che pur mantenendo i principi del precedente risulta essere meno oneroso.
La stessa condotta che unisce i due serbatoio (arteria principale) fa da distributrice.

Altri tipi di distribuzione

In città pianeggianti dove non esiste la possibilità di serbatoi in quota si ricorre, sovente a serbatoi pensili.
Questi hanno modeste capacità e pertanto non possono alimentare l’intera rete cittadina. Ciascuno avrà una propria zona di influenza.
Essi a loro volta potranno essere alimentate di un’arteria od un anello che nel caso di figura é alimentato da una stazione di spinta. Ne segue lo schema qui riportato.

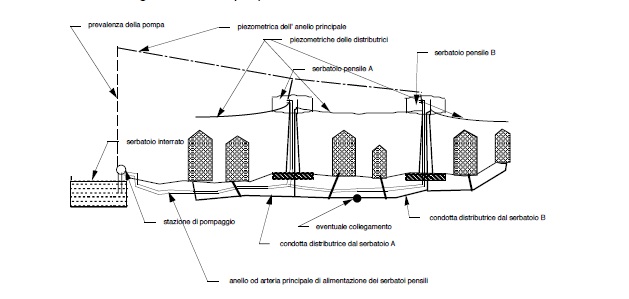
Le reti distributrici dei vari serbatoi possono essere tra loro ricollegate ( ma é sempre opportuno che i collegamenti non siano plurimi (cioè più condotte che ricollegano gli stessi serbatoi) onde facilitare, come già detto operazioni di manutenzione e/o di esclusione dal servizio di un serbatoio.
Ben poco vi é da dire sulle reti aperti che alimentano frazioni isolate, case sparse, tipiche degli acquedotti rurali. E3 solo opportuno, ove possibile che anche in questi casi vengano realizzati, in quota o pensili dei serbatoi anche modesti.

Con tali opere che in questi casi assolvono più a compiti di sconnessione
che a quelli di stoccaggio si suddivide la condotta in tratti con compiti di solo trasporto dell’ acqua (con qualche modesta distribuzione lungo il percorso), a compiti di esclusivo trasporto.
Eventuali sprechi dovuti a consumi impropri (irrigazione di orti) che spesso
in tali acquedotti vengono a verificarsi sono così se non impediti, contenuti negli effetti : non può essere sprecata più acqua di quelle che contenuta nel serbatoio.
Più complesso é il caso di città più o meno grandi che presentino grandi
dislivelli e conformazione morfologica più o meno complessa.
Una di queste città é certamente Ancona che presenta entrambi i problemi:

grandi dislivelli;
conformazione complessa
E’ evidente che in casi analoghi ben difficilmente uno schema di quelli prima esaminati possa adattarsi sic et simpliciter. Le città con notevoli dislivelli altimetrici occorrerà vengano divise in più zone,ciascuna con dislivelli (tra i piani di campagna) non superiori ai 40÷50 metri.

Ciascuna di queste zone dovrà avere una propria rete di distribuzione del tutto indipendente da quella delle altre zone (salvo eventuali collegamenti di emergenza). Ciascuna rete dovrà avere un proprio serbatoio posto ad idonea quota sul piano di campagna medio della zona da servire. In particolare non é opportuno che in ciascuna rete si superino in rete pressioni pari ad 80 metri di colonna d’acqua. Valori maggiori oltre a dare fastidio agli utenti che peraltro devono stare molto attenti agli effetti dei getti sugli oggetti che portano sotto i rubinetti per il lavaggio ecc.. compromettono la tenuta dei rubinetti in genere ed in particolare di quelli a chiusura automatica quali quelli di lavatrici, lavastoviglie ecc…
Pertanto la prima precauzione di un acquedottista sarà quella di individuare su una carta a curve di livello le diverse zone, comprese tra due isoipse che possono essere alimentate dallo stesso serbatoio, progettando per ciascuna di esse una apposita rete distributrice.
Se la città si presenta morfologicamente complessa sono necessari studi dettagliati per individuare la suddivisione in reti diverse. Si é già detto di Ancona che presenta una zona (a sua volta da suddividere in varie sottozone in funzione della quota) delimitata dal displuvio del collettore naturale che dal Passetto, percorrendo viale della Vittoria e poi Corso Garibaldi giunge al porto, ed un’altra zona al di qua della “galleria” anch’essa a sua volta da suddividere in varie sottozone in funzione della morfologia e della quota, per esempio la zona di valle Miano, il Piano, ecc.
Ma Ancona non é un caso isolato, anche altre città necessitano di svariate reti di distribuzione in funzione dello loro complessità morfologica, qui citiamo Roma e Napoli, ma l’ elenco potrebbe essere lunghissimo.
Di certo ognuna delle dette reti, singolarmente si ispirerà ad uno schema più
o meno classico adattandolo alla circostanza o meglio alla morfologia locale.
Scarso effetto in questa fase progettuale deve avere l’altezza media degli
edifici, infatti é ovvio che l’acquedotto pubblico dovrà poter servire gli utenti senza ulteriori rilanci (necessità di ulteriori pompaggi) di acqua.
Ma chiaramente un tale servizio non potrà essere prestato in quelle zone dove sono stati (o saranno realizzati) edifici di grande altezza (edifici a torri, grattaceli ecc…)
Possiamo ammettere che direttamente l’acquedotto possa alimentare edifici sino a 5÷6 piani. Vale a dire sino a 15÷18 metri dal piano di campagna.
Infatti tenuto conto che affinché l’acqua fuoriesca da un rubinetto con la necessaria energia é necessario che abbia immediatamente a monte di questo una pressione di 5 metri di colonna d’acqua . Ne segue che ai piedi dell’ edificio posto nella zona più alta delle rete distributrice dovrà avere una pressione di circa 25 metri di colonna d’acqua (tenuto conto delle perdite di carico) e quindi se la zona più alta ha quota di 50 metri superiore a quella più bassa, tenuto sempre conto delle perdite di carico, risulta che il distribuzione sarà necessario appunto una pressione massima di 80 metri di colonna d’acqua. come in precedenza indicato.

La realizzazione delle reti di distribuzione

La figura che segue illustra un esempio di realizzazione di distribuzione.

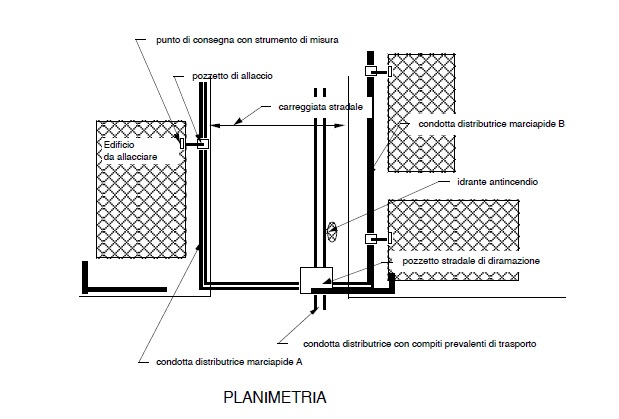
Fin tanto che la condotta distributrice ha un diametro superiore ai 100 mm si riene non opportuno che svolga copiti effettivi di distribuzione cioé che venga ampiamente sforacchiata per prelievi d’acqua da parte di utenze (cioé con condote di allacciamento).
Si può invece realizzare una distribuzione del tipo di quella sopra schematizzata, che peraltro ha in vantaggio di evitare contiui tagli ed attraversamenti delle sede stradale con condotte di allaccio.
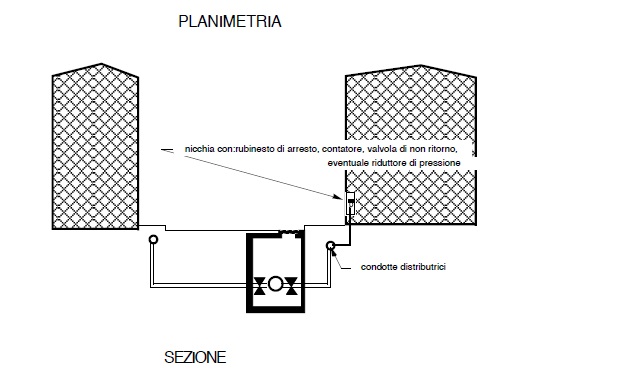
All’ uopo si collocano delle condotte di diametro modesto, in genere in PEAD, al di sotto dei marciapiedi, dalle quali si dipartono gli allacci alle utenze. Tali condotte sono poi ricollegate con la distributrice cittadina in appositi pozzetti di diramazione.
Tale razionalizzazione comporta un maggior onere di costruzione ma gestioni molto più semplici e con costi molto minori.
L’eventuale rifacimento delle distribuzioni, oggi tali reti sono le più deteriorate e maggiormente necessitanti di interventi manutentori) deve poter servire anche per razionalizzazione il punto di consegna (che deve essere dotato, in generale di valvola di non ritorno, di rubinetto d’arresto, di eventuale riduttore di pressione e di strumento di misura: contatore).
Tale punto di consegna deve avvenire il luogo facimente accessibile dalla pubblica via in modo da facilitare lettura dei contatori ed eventuali altri interventi degli uffici preposti alla gestione dell’ acquedotto.
Lungo la rete di distribuzione é poi necessaria la presenza di idranti antincendio, che sono posti nella immediataprossimità di condotte distributrici di diametro e pressione adeguata e sono riconoscibili dai chiusini a forma ovale (quando non trattasi di idranti esterni all’ americana).

Cenni alla necessità di sollevamento d’acqua negli edifici

Si é già detto che le reti di distribuzione pubblica non possono alimentare direttamente edifici alti o grattaceli.
In tal caso sarà compito del proprietario dell’ edificio (condominio) provvedere a che l’acqua prelevata dall’ acquedotto pubblico possa giungere anche ai piani più alti della torre.
Infatti stando alla rete distributrice cittadina, la piezometrica taglierà in due l’edificio a torre, come illustrato in figura.

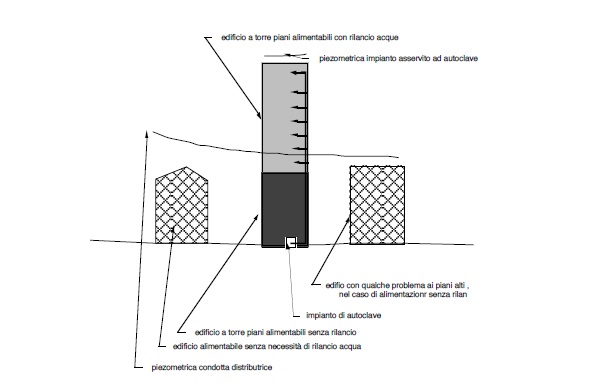
Dalla stessa si evinca come una parte dell’ edificio potrebbe ancora essere alimentata direttamente dall’ acquedotto ed un’altra dovrà necessariamente essere alimentata tramite autoclave.
DI norma si verifica che poi tutto il condominio verrà alimentato da autoclave.
In quanto segue non ci si vuole soffermare sul dimensionamento di queste, peraltro non difficile, ma su alcune questioni che più da vicino riguarda non il servizio acquedottistico.
E’ estremamente importante :
a) che tra serbatoio a monte dell’ autoclave, vedi figura seguente, rete idrica citta daina vi sia un riduttore di pressione
b) che non siano presenti by-pas al sistema autoclave.
Quest’ ultima é una norma di tipo igienico che serva a non far ritornare in rete acque già entrate nella rete idrica del condominio
La prima invece serva a far si che la piezometrica cittadina non si adegui al livello idrico del serbatoio.
A monte del riduttore di pressione vi possono essere le prese per la parte di condominio alimentabile senza autoclave. E’ ovvio che se il condominio é una torre di diversi piani possono essere necessari più impianti di sollevamento.

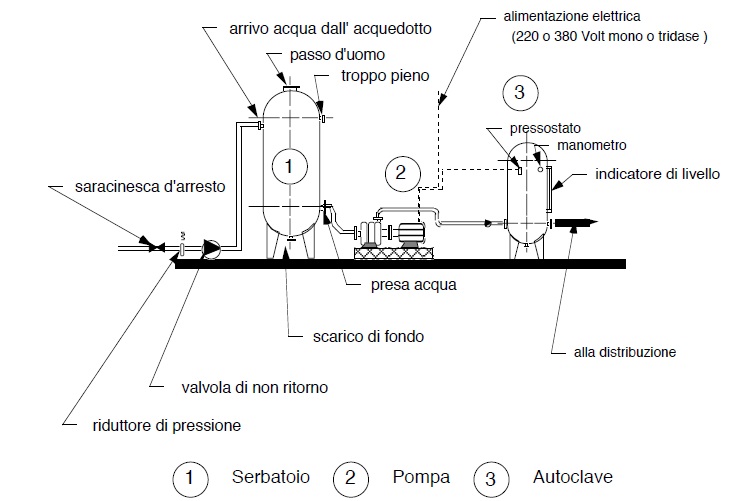
Circa la progettazione di tali impianti di autoclave come pure sulle altre opere d’arte esi rimanda agli appositi capitoli delle presenze dispense.

Il dimensionamento delle reti di distribuzione

Per dimensionare una rete distributica occorre tener conto :
a) della portata che ciascun tratto della rete deve erogare alle utenze nel momento di massimo consumo;
b) della quantità che ciascun tratto deve trasportare per rifornire la rete a valle;
c) la pressione che in ciascun tratto, espressa in metri di colonna d’acqua ( almeno superiore di 5 metri all’ edificio più alto);
d) inoltre va tenuto conto, soprattutto nei piccoli centri della necessità di prevedere ed installare, anche in periferia, di idranti antincendio, i quali per poter funzionare richiedono portate dell’ ordine di 5÷10 l/s e pressioni di almeno 3 atm.
Per tali motivi le distributrici del IV ordine non dovrebbero mai avere diametri interni inferiori ad 80 mm (ma se sono previsti idranti il diametro non é consigliabile scenda al di sotto di 10 mm). Le diramazioni di ordine superiore a quello prima indicato possono anche non essere soggette a calcolo (va comunque verificato che a monte della diramazione di sia pressione sufficiente).
Uno dei problemi più difficoltosi da affrontare é quello della stima delle portate che la rete deve distribuire lungo il percorso.
A tal fine sarebbe necessario conoscere la distribuzione degli utenti strada per strada. Tali informazioni possono essere tratte dall’ anagrafe. Detta Q_i la portata complessivamente distribuita dall’ i-esimo tronco di distributrice, lungo L_i , lungo il quale sono distribuiti P_i abitanti, avremo:

dove:
P é la popolazione dell’ intero centro e
Q_a é la portata media annua
Ne segue che la portata q_i per unità di lunghezza, varrà:

La valutazione della q_i come sopra indicato é piuttosto complessa in quanto fa riferimento appunto alla distribuzione P_i della popolazione.
Un altro metodo, più pratico ma meno preciso, é quello di suddividere la città in zona di pari densità abitativa. Sia c_i un parametro che esprime la densità di popolazione nella strada iesima sita nella j-esima zona, ne segue che avremo:

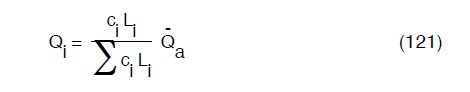
o, in termini di portate per unità di lunghezza, avremo:

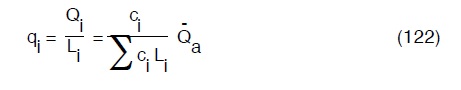
Come nella quasi totalità dei problemi di ingegneria non esiste un vero e proprio calcolo di progetto.
Si giunge al dimensionamento per:

via sintetica (per similitudine con casi analoghi),
o
basandoci grossolanamente su diametri atti a contenere entro determinati valori (max 2 m/s) le velocità delle portate fluenti
oppure
tramite l’esperienza maturata.

Il criterio cui occorre informare il dimensionamento é quello di un anello principale di pari diametro alla condotta di avvicinamento¹⁰ avendo cura che in quest’ultima le velocità non superiori i 2 m/s
Fissato il diametro dell’ anello principale e fissate le portate uscenti da ciascun nodo, é poi possibile stabilire “a sentimento” i diametri delle distributrici dal II al IV ordine che vanno poi sottoposti a procedimento di verifica.
In vero si potrebbe impostare il seguente calcolo di dimensionamento che ha la sua logica in un criterio di economia consistente nel minimizzare il costo relativo all’ anello principale ed alla sole condotte del secondo ordine:

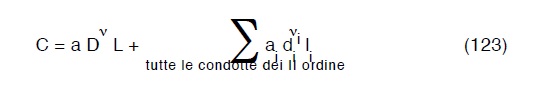
con :

sotto le condizioni che siano fissati i dislivelli piezometrici h_i tra serbatoio S ed estremità della i-esima condotta secondaria. Per h_i potremmo dunque scrivere :

₁₀ Sassoli e Milano. Il Giornale del Genio Civile 1973, hanno dimostrato tuttavia la convenienza (economica) di diametri diversi allorquando la condotta di avvicinamento é di lunghezza considerevole.

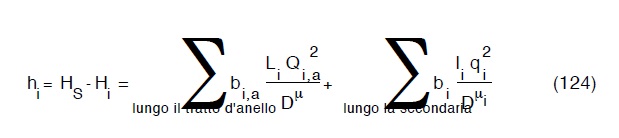
ponendo dunque:

la (126) diventa:

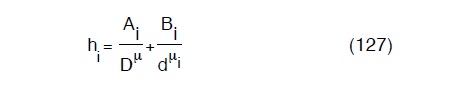
Adottando il metodo dei moltiplicatori di Lagrange, avremo dunque:

Che va derivata rispeeto a ciascun d_i oltre che rispetto a D ed i relativi risultati eguagliatoi a zero, avremo dunque:

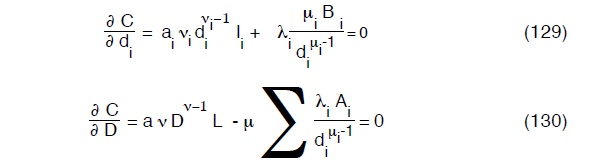
Ricavando i valori di λ_i dalle (129) :

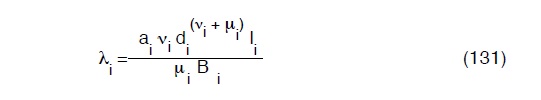
e sostituendoli nella (130), avremo:

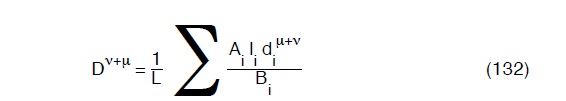
Il sistema costituito dalle :

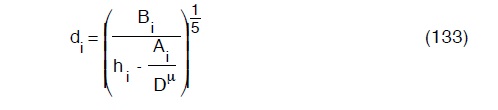
e dalla (132) é risolvibile previa linearizzazione con i metodi del calcolo numerico. Un tempo la si risolveva, per tentativi tramite l’organizzazione di tabelle ad hoc.
Si fissava un diametro D, di tentativo, per l’anello principale con l’unica condizione che i denominatori delle (133) siano positivi. Quindi si calcolano i valori di d_i.
In generale la (132) non sarà verificata, dalla quale potremo calcolare il valore D’ . Come valore di secondo tentativo adotteremo un valore intermedio tra D e D’ e così di seguito sin tanto che non si otterranno scarti D’-esimo – D’-esimo+1 tecnicamente insignificanti.
La tabella che segue da un’ idea di come può essere organizzato un tale calcolo in maniera manuale o con solo foglio elettronico.

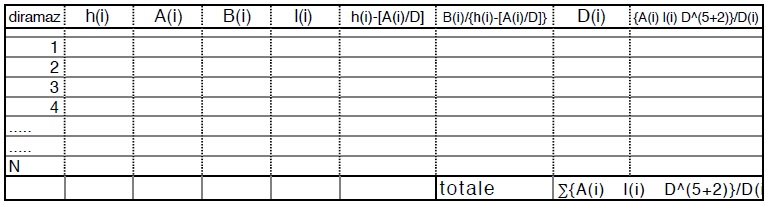
Non ci soffermiamo oltre sull’ argomento. accenniamo solo che anche su tale argomento, come su quello affrontato appena oltre cioé della verifica, negli ultimi anni, cioé dall’ avvento dei computer, sono stati tentativi di ottenere softwar risolutori del problema.

Citiamo i lavori di Cenedese (Convegno di Idraulica e CostruzioniIdrauliche di Roma del 1976) e di Artina (Convegno di Idraulica e Costruzioni Idrauliche di Bologna del 1982) ma nessuno di questi é mai stato effettivamente risolutore anzi non é stata a tutt’oggi non solo provata l’unicità della soluzione ma
appunto neppure una qualche soluzione soddisfacente¹¹.

¹¹ Si confronti PILATI e TODINI, Istituto di Costruzioni Idrauliche, Bologna …..

La vericica delle reti di distribuzione

Releghiamo volutamente ed in una nota il più classico dei metodi per la verifica delle reti idrauliche, quello di Hardy Cross¹² e trattiamo l’argomento con il

¹² Hardy Cross, nato nel 1895 e scomparso nel 1959 fu professore di Scienza delle Costruzioni in diverse Università americane (Illinois state University ed Virginia University). E’ autore di molti metodo i numerici per la soluzione approssimativa di grandi sistemi di equazione tipiche dell’ ingegneria non che di metodi numerici di linearizzazione.
Ha legato il suo nome oltre che al metodo sopra accennato anche ad un classico metodo per la soluzione di telai strutturali. Per le reti idrauliche il problema affrontato da Cross é scindibile in due :
I) linearizzazione di equazioni del secondo ordine;
II) risoluzione iterativa di un sistema pseudo lineare di diverse equazioni.
In generale può farsi riferimento allo schema che segue, necessariamente limitato a soli due anelli.

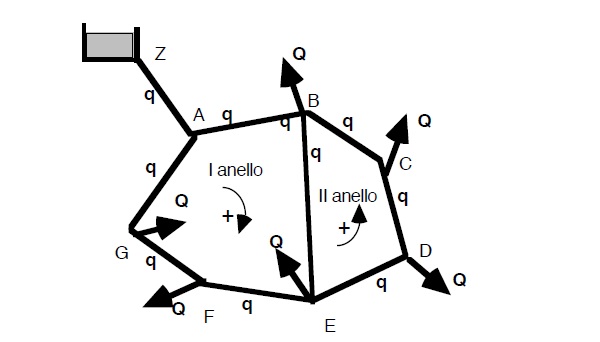
Detto h_i la perdita di carico nel i-esimo lato delle j-esimo anello della rete da verificare, avremo:

dove volutamente si adotta per L_i il segno positivo se assumiamo che esso sia percorso dall’ acqua nel verso positivo e veceversa nel caso opposto. Ovviamente, stante la precedente ipotesi, sarà:

In ciasscun nodo della rete dovrà inoltre essere verificata l’equazione di continuità

Questa operazione viene fatta “a sentimento” assegnando a ciascuna portata di tipo q un valore di tentativo plausibile (le portate di tipo Q sono ovviamente note). Sostituendo la (i) nella (ii)

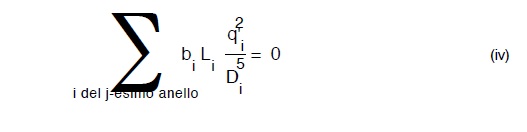
ed introdotti in essa i valori di tentativo di q’_i questa non sarà in generale verificata. Lo sarà invece la (v i) dove al posto di q’_i é stato posto il valore corretto q_i ottenuto tramite la:

dove Δq_j é la correzione delle q’_iper il j-esimo anello ( é banale convincersi che la correzione é unica per tutti i lati di un anello: infatrti é ovvia conseguenza dell’ equazione di ointinuità (iii) ) segue dunque la

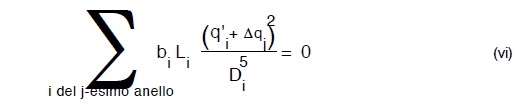
o, che é lo stesso la :

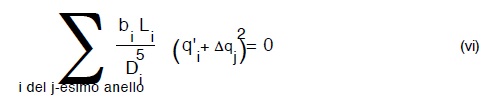
Sviluppando il quadrato del binomio che compare sotto segno di sommatoria, avremo:

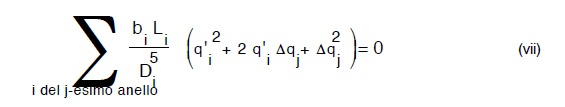
Se i valori di q’_i non sono troppo lontani dal vero, allora Δ_qsarà piccolo ed a maggior ragione lo sarà Δq²_j, pertanto la (vii) é semplificabile nella :

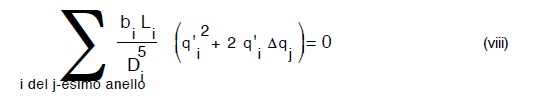
dalla quale ovviamente avremo:

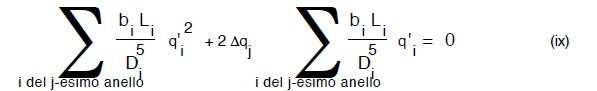
ora tenuto conto che nella (ix) l’unica incognita é appunto la correzione Δq_j_, possiamo risolverla nella:

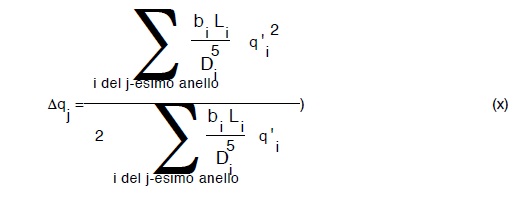
Difficilmente la soluzione data dalla (X) sarà quella esatta, in quanto l’approssimazione fatta (cioé il trascurare il quadrato della correzione Δq_j non sarà in generale ammissibile. metodo generale dell’ analisi topologica.
E’ tuttavia necessaria una premessa di ordine storico.
Sina a circa metà degli anni “60 il metodo di Cross fu quasi incontrato dominatore del settore. Ma con l’avvento dei computer e le diverse possibilità che questi offrivano e nella sintetizzazione delle reti e nella formulazione stessa del procedimento risolutivo, il metodo di Cross é stato di gran lunga superato anche se non mancarono tentativi (Iannelli, 1963 e 1967) di implementarlo su computer.
A tutt’oggi si trovano sul mercato software che implementano il Cross per reti idrauliche o di metano ma trattasi sempre di procedimenti di gran lunga superati, che trovano ancora qualche applicazione a causa dell’ inerzia dei professionisti ad affrontare il problema in termini più corretti.
Si devono a Chandrashekar (Asce Journal of Hydraulic Division, 1972 e 1975) i primi approcci al problema, costituito da un sistema di equazioni non lineari, risolvendolo con il metodo iterativo di Newton-Raphson.

La soluzione esatta la si ottiene reiterando la (x) dopo aver apportate alle q_‘ile correzioni Δq_j.
Il problema di verifica sarebbe così risolto se l’anello fosse soltanto uno, ma in generale gli anelli sono di più. In vero all’ epoca di utilizzo di tale metodo i progettisti facevano ogni sforzo per limitare ad un numero compatibile con il calcolo manuale il numero di aneli da sottoporre a verifica. Quello sino ad ora risolto é solo un problema di linearizzazione. Nel caso di presenza di più anelli, risolto il primo si passa alla soluzione del secondo, poi del terzo ecc… Ogni soluzione porterà delle correzioni del tipo Δ_jche andranno portate anche al lato comune agli anelli contigui e già risolti (é il caso del lato BE della figura precedente).
Risolti per la prima volta tutti gli anelli, si ritorna a risolvere il primo , ovviamente dopo avervi apportato le correzioni Δq_j provenienti dalle soluzioni degli altri anelli.
La soluzione la si ottiene dunque per via iterativa dopo almeno 3 o 4 “giri” I calcoli si conducono abbastanza celermente se li si organizzano in tabelle, vere precursitrici dei fogli elettronici attuali, tramite i quali é possibile risolvere oggi il problema alla Cross.

WOOD e CHARLES nel 1972 hanno risolto il sistema ottenuto con la teoria dei grafi usando le tecniche dell’Analisi Lineare¹³, cioè linearizzando come segue:

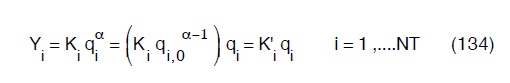
dove q_i,0 è il valore approssimato della portata nel tronco iesimo.
Tali metodi sono stati ripresi in Italia dapprima da Curto ed altri (XV Convegno di Idraulica a Costruzioni Idrauliche, 1976- Roma, poi da Mantica e Ribighini (Giornale del Genio Civile , 1979) e quindi da Todini sempre nel 1979. E’ a quest’ultimo che si deve la soluzione generale del problema. Questi infatti ha impostato il problema come un problema di equilibrio e ne ha cercato la soluzione stabile minimizzandone l’energia in gioco. Ha quindi ottenuto un sistema univocamente determinato anche da un punto di vista numerico e quindi una soluzione rispondente sempre alla soluzione del problema fisico, cosa che a volte, con gli altri procedimenti non si otteneva (infatti trattandosi di un problema non lineare questo in generale ammette oltre che la soluzioni fisica anche altre solo matematiche¹⁴). CONTRO e FRANZETTI, nel 1980, impostando ancora il problema come il l Todini ma usando un algoritmo diverso (regola di coniugazione delle direzioni ammissibili), permettono di inserire espressioni non monomie delle perdite di carico. E’ poi da citare anche il POGGI che ha messo a punto, nel 1985, un metodo che si propone di raggiungere la distribuzione delle portate di regime permanente mediante un procedimento di integrazione del le equazioni di moto vario in ciascun ramo usando la teoria delle linee caratteristiche già applicata da

¹³ Un precedente approccio con il metodo dell’ analisi lineare é dovuto a Shamir e Howard (1968) in “Water distribution sysetm analysis” Jr of Hydraulic Div. ASCE Vol . N/ro 94 pag 219-234
¹⁴ Come riscontrato da Carlo CAO (1963 – VIII Convegno di Idraulica e Costruzioni Idrauliche di Pisa)per il metodo di Cross, e da MANTICA e RIBIGHINI (1982 – IV Conferences internationale sur la planification et la gestion des eaux IV Conferences internationale sur la planification et la gestion des eaux.Marseille F) per i metodi basati sull’ Analisi lineare.

EVANGELISTI, in maniera soddisfacente, allo studio del colpo d’ariete.Trattasi però di procedimento, quest’ultimo non entrato nella pratica cossente, ma utilissimo per sitazioni particolari.
In sostanza oggi disponiamo di due metodi per la soluzione del problema di verifica:

il metodo del gradiente coniugato;
il metodo dell’ analisi lineare.
Qui di seguito verranno esposti entrambi.
Un confronto tra i due metodi é stato portato avanti da Mantica e Savini (1992) ne é risultato che il metodo del gradiente coniugato gode di una maggiore celerità di soluzione.

Impostazione del problema in termini topologici

Nel precedente punto si é già impostata la definizione di una rete acquedottistica in termini topologici. Il caso trattato nel punto menzionato faceva espresso riferimento ad acquedotti consortili, ma ovviamente le (70) e le (71) valgono anche per le reti di distribuzione.

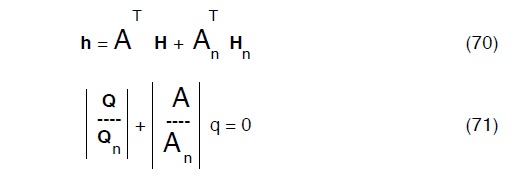
dove A é la matrice topologica definita come nel punto menzionato dove peraltro sono definiti anche gli altri termini matriciali delle (70) e (71).
ll vettore h che rappresenta la perdita di carico nei vari lati della rete, avrà generica espressione:

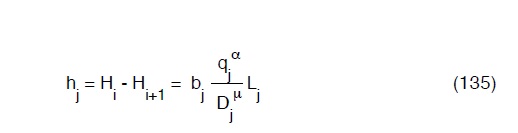
Tenuto conto che b_j

sono delle costanti che possiamo indicare con r_j, ponendo quindi :

avremo

che sostituito scritta in termini matriciali e sostituita nella (70) porta il problema (70) e (71) ad un problema, determinato, nelle sole q, non lineare

Il metodo dell’ analisi lineare

Il metodo dell’ analisi lineare si basa sulla seguente trasformazione della(137).
Si ponga :

ne segue che la (137) si trasforma nella:

o, che é lo stesso

Introducendo ora una matrice quadrata Y con i soli elementi diagonali non nulli, ed il cui generico elemento diagonale sia:

la (139) diviene:

ed, in forma matriciale:

che sostituita nella (71) riporta il problema ad uno pseudo-lineare¹⁵nelle sole h.

e tenuto conto della (70) avremo:.

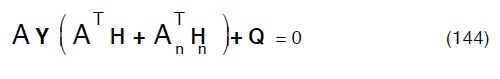
posto dunque.

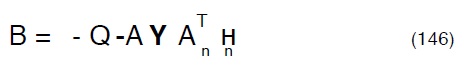
segue la:

¹⁵ La formulazione sopra esposta del metodo dell’ analisi lineare é quella di Curto, invero per una corretta analisi lineare occorrerebbe calcolare loJacobiano, cioé le derivate prime di ciascuna equazione fatte rispetto alle varie variabili ed assumerle come coefficienti del sistema linearizzato.
Ma di fatto otterremo un sistema di coefficienti identico a quello sopra indicato a meno di una costante.

La (147) può essere risolta con uno dei tanti metodi dell’ analisi numerica per i sistemi lineari¹⁶.
Ottenuta una soluzione h, questa va sostituita nella (141), quindi a ciascuna iterazione corrispondono nuovi valori delle q_j e nuovi valori della matrice Y. Si risolve quindi nuovamente la (142).
Il procedimento si arresta quando i valori delle portate ottenute tramite due elaborazioni successive differiscono di entità sufficientemente piccole. A differenza del metodo di CROSS non è necessario fare una stima della distribuzione iniziale delle portate.
Gli autori hanno calcolato la soluzione iniziale supponendo, in prima approssimazione, che la K_‘i della (134) sia indipendente dalle portate. Questa ipotesi, però, risulta essere valida solo nel caso del moto laminare,
quindi non sempre è accettabile; inoltre tale metodo richiede la memorizzazione di matrici di grandi dimensioni allorquando lo si applica a reti complesse, pertanto non è sempre agevole il suo utilizzo.

CURTO tenendo conto che la matrice dei coefficienti del sistema di equazioni pseudolineari è simmetrica, sparsa, definita positiva e facilmente diagonalizzabile¹⁷, superano tale limitazione con un procedimento di riduzione a banda della matrice e quindi con conseguente notevole risparmio di memoria.
MANTlCA e RlBlGHINl hanno apportato delle modifiche al metodo di CURTO affinché il problema di verifica diventi un problema di simulazione onde ottenere indicazioni utili per la gestione della rete, inoltre hanno introdotta la possibilità di tener conto della presenza di distribuzione idrica lungo i tronchi, di perdite di carico concentrate, di serbatoi sussidiari, nonché viene previsto

¹⁶Escluso, date le dimensioni il metodo di inversione della matrice sono adottabili il metodo di Gaus, quello di Gaus-Seidel, di Jacobi, di overlassaazione e di surrilassamento
¹⁷ La matrice C espressa dalla (145) gode della seguente proprietà (Mantica, 1979, loc. cit.)

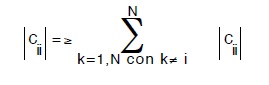
l’eventuale inserimento di pompe nella rete.
CALOMINO e VELTRI hanno inserito tra le incognite le portate in ingresso e in uscita in quanto dipendenti dalla piezometria della rete, anch’essa incognita.

Il metodo del gradiente coniugato di Todini

Tutti i metodi sopra menzionati sono non lineari e possono presentare fenomeni di instabilità numerica, nel senso che non sempre la soluzione ottenuta coincide con la soluzione fisica del problema.
TODINI ha dimostrato come la soluzione del problema di verifica coincida con il minimo della potenza dissipata P_d nella rete, nel rispetto dei soli vincoli di continuità ai nodi.
Tale criterio trova fondamento nel principio ben noto della stabilità dell’equilibrio dinamico.
Applicando dunque il metodo del gradiente coniugato al sistema non lineare ottenuto con il predetto criterio, TODINI ha messo a punto un metodo di verifica che arriva alla soluzione indipendentemente dai valori di partenza.
E da notare che, in questo caso, le variabili del problema, cioè portate e carichi, sono determinate simultaneamente, rispettando così maggiormente l’interazione che realmente esiste tra le variabili.
L’ energia dissipata da un generico lato della rete é dato dalla:

quindi l’energia totale dissipata dalla rete sarà:

Per il principio dei lavori virtuali¹⁸ otterremo la soluzione di equilibrio imponendo il minimo della (149) o , che é lo stesso della:

sotto le condizioni espresse dalla (71).
Si introduca all’uopo un vettore colonna λ di tanti componenti quanti i nodi della rete costituenti i moltiplicatori di Lagrange da associare alle (71) avremo che la funzione da minimizzare L(q,λ) sarà :

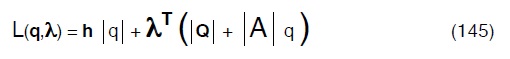
e, tenuto conto della (137) avremo:

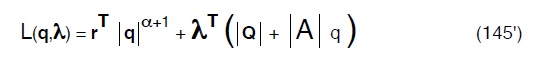
derivando sia rispettp a q che a λ ed eguagliando a zero:

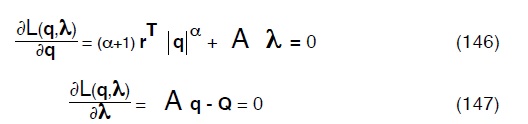
Considerando poi che¹⁹ :

¹⁸ Si confronti R. Einaudi “Meccanica Razionale” vol II pag. 294 edizioni Pellegrini, Pisa 1967.
¹⁹ Infatti dalla 141 , esplicitando in y_jj avremo:

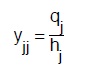
e tenuto conto della (137) avremo:

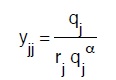
avremo:

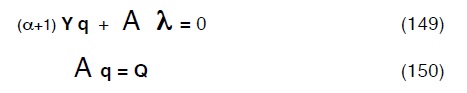
Occorre dare forma matriciale anche ai coefficienti del sistema: la presenza di un vettori partiti in due sia per le incognite che per i termini noti porta a dedurre che la matrice del sistema sarà partita in quattro20.
Il primo quadrante conterrà i coefficienti della (149) relativi alla variabile q, quindi (α+1) Y.
Il quarto quadrante conterrà i coefficienti della (149) relativi alla variabile λ,

da cui

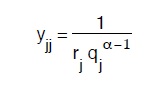
ne segue la (148).

²⁰Nel seguito indicheremo con verso antiorario i quattro quadranti della matrice partita, cioè secondo lo schema seguente:

quindi A.
Il secondo quadrante conterrà i coefficienti della (150) relativi alla variabile q, quindi A.
Il terzo quadrante conterrà i coefficienti della (150) relativi alla variabile λ, quindi 0.
La matrice dei coefficienti sarà dunque la :

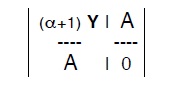
ed il sistema sarà quindi dato dalla :

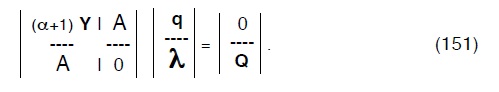
Posto poi

segue che il sistema (151) si modifica nella²¹ :

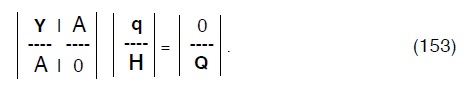
La (153) non é lineare e pertanto per essre risolta va linearizzata, il Todini propone il metodo del gradiente coniugato (e dall’ uso di tale metodo prende il nome il presente procedimento di verifica delle reti).

²¹ Eseguendo il prodotto matriciale della (153) tra partizioni, avremo:

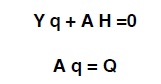
la prima di queste, confrontata con la (144) ci porta a concludere che H altro non é che il carico idraulico (altezza piezometrica) ai nodi.

Derivando avremo:

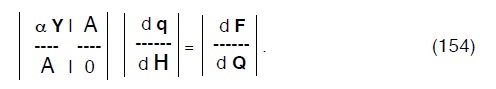
dove:

e l’indice sta ad indicare l’i-esima iterazione
Posto ora:

Dove :

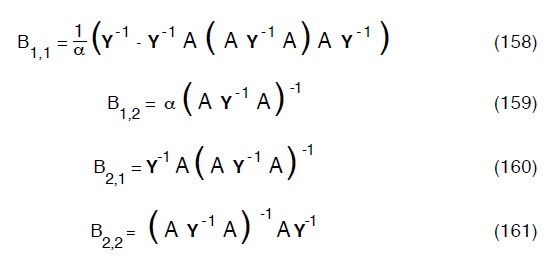
sostituendo la (157) nella (154), tenuto conto della (155) e (156) avremo:

ed infine:

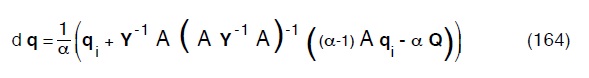
che risolvono il problema di verifica, ovviamente sempre per via iterativa.
Ammettiamo ora di conoscere una soluzione q_i congruente, cioé che rispetti l’ equazione di continuità²² (71). Sostituendo la (71) nella (164) e (165) avremo:

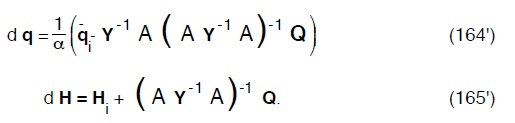
ora, tenuto conto che:

avremo il seguente algoritmo ricorsivo:

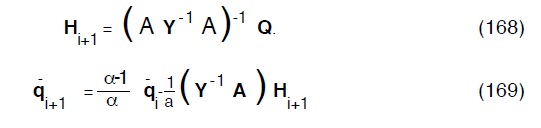
Di fatto quindi il problema é ricondotto alla soluzione del sistema (168) in quanto la (169) é immediata allorquando sia noto H_i+1
.La (168) a sua volta può essere esplicitata nella:

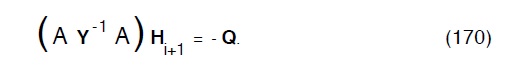
formalmente analoga alla (147) del metodo dell’ analisi lineare, che quindi può essere scritta nella forma:

²² La qual cosa la si ottiene risolvendo il sistema:

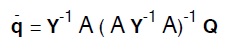
o, posto

nella equivalente:

La differenza tra i due metodi consiste nella espressione con la quale
ottenere il valore di q

i+1

Questo infatti nel metodo di Todini é dato dalla (169) mentre nel metodo dell’ Analisi lineare l’ espressione corrispondente é la (142). Tale differenza é tuttavia estremamente importante e perché da stabilità
fisica alla soluzione del problema e perché lo velocizza. Per risolvere il sistema lineare costituito dalle (170) il Todini preso atto delle dimensioni e proprietà della matrice

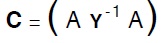
che sconsigliano e il metodo di Gaus e l’inversione della matrice propone il metodo del gradiente coniugato di Hestness e Stiefel.
La (174) viene quindi ricondotta alla minimizzazione del funzionale F(X) definito dalla :

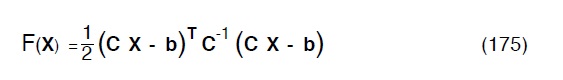
sviluppando i calcoli, otteniamo:

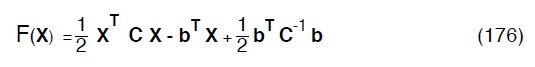
Tenuto conto che la (176) va derivata rispetto ad H possiamo sostituirla con il funzionale F’ (X):

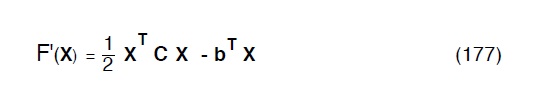
Posto ora:

nonché:

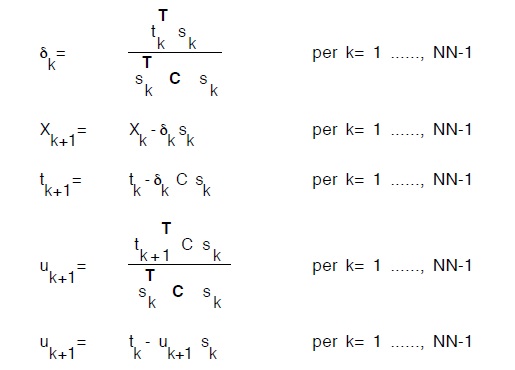
Risolto il problema in X e quindi in H_i+1 é poi possibile tramite la (168) e (169) risolvere in toto il problema.

²³ Todini dimostra che, in linea teorica, al più il numero di iterazioni sarà pari ad N.

Gli altri metodi come derivati dal metodo di Todini.

Il metodo di Cross.

Se moltiplichiamo la (153) che é l’equazione generale delle reti

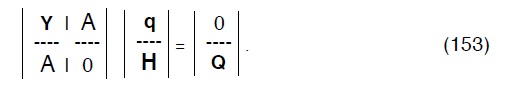
per una matrice topologica di ordine [NT * (N*NT) ] che descrive le maglie della rete, e che quindi sia del tipo

con:
NT numero dei tronchi
NN numeri dei nodi
M_i,m che vale:

1 se il tronco i appartine alla maglia m e verso concorde quello prefissato per la maglia;
0 se il tronco i non appariene alla maglia;
-1 se il tronco i appartine alla maglia m e verso non concorde quello prefissato per la maglia;

NM numero delle maglie;
I matrice identità di ordine [N*N]
e dove la sottomatrice M deve ovviamente verificare la:

avremo:

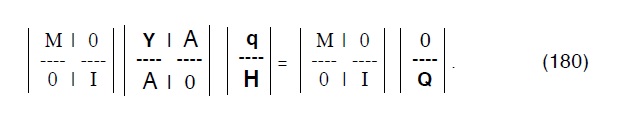
ne segue:

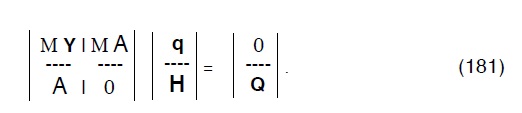
e tenuto conto della (179), avremo:

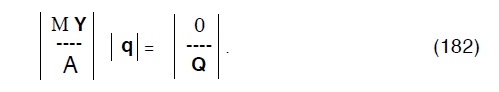
che altro non é che il sistema alla Cross scritto in termini matriciali,con complessivamente una dimensione N*N Purtoppo le singole matrici MY e A non sono quadrate per cui non é possibile operare facilmente con i metodi prima visti e Cross agira il problema operando con un gradiente locale (maglia per maglia).
E’ da notare che il metodo di Cross sarebbe in teoria, dunque anch’esso ad unica soluzione derivando da quello generale (153) tramite una trsformazione lineare convessa. I problemi di non convergenza posti in evidenza da Cao sono dunque dovuti a problemi di instabilità numerica dell’ algoritmo adottato da Cross.

Il metodo dell’ Ansalisi lineare.

Si é già fatto notare come la differenza tra i due metodi consiste esclusivamente nella diversa formulazione delle equazioni (169) del Todini e la (142) di Wood e Charles :

diventa

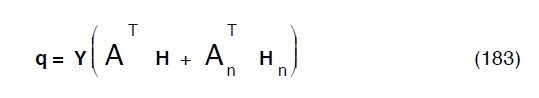
Quest’ ultima é ottenibile dal sistema generale (153) moltiplicandone ambi i membri per la matrice

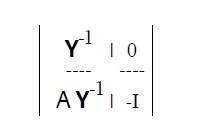
con significato dei simboli già introdotto.
La formulazione (183) ha, come già detto problemi di convergenza che si manifestano qualora la soluzione iniziale della h_j non sia buona24.

²⁴ Curto per le h_i iniziali propone di porle pari all’ unità, tale soluzione iniziale può dare dei problemi che in parte possono essere risolti con un valore iniziale proporzionale alla lunghezza L_j del tronco come proposto da Mantica e Ribighini (1982, loc. cit.)

PROMOTECNICA RC

Soluzioni innovative per il “Ciclo integrato dell’Acqua” “Ambiente” – “Industria”