
I serbatoi sono dei depositi dove viene accumulata l’acqua nei periodi in cui la sua produzione7 supera il fabbisogno e dai quali viene prelevata quando il rapporto produzione/consumo si ribalta.
Più specificatamente, dal punto di vista dello scopo, possiamo distinguere i
serbatoi in:
- serbatoio di compenso;
- serbatoi di riserva;
- serbatoi antincendi.
Ovviamente ad un serbatoio possono essere assegnati od uno solo o, più sovente, più di uno degli scopi sopra indicati.
Ovviamente ad un serbatoio possono essere assegnati od uno solo o, più sovente, più di uno degli scopi sopra indicati.
Ovviamente a seconda dei casi sarà diverso il dimensionamento volumatrico (o dimensionamento idraulico).
Oltre che dal punto di vista del dimensionamento idraulico, i serbatoi vengono distinti a seconda del rapporto tra gli stessi e la superficie topografica in :
a) serbatoi a cielo aperto,
b) serbatoi a cielo chiuso.
I primi, una volta erano praticamente inesistenti in campo acquedottistico, oggi invece sono sempre più frequenti e lo saranno tanto di più quanto più frequente sarà il ricorso ad approvvigionamento da acque superficiali. Sono invece tipici dei serbatoi per impianti idroelettrici; per irrigazioni ecc…
Tra essi distinguiamo in :
- serbatoi semi naturali realizzati sbarrando con una diga una vallata
esistente: - serbatoi artificiali, realizzati costruendo vasche tramite
7 Termine inteso nella sua accezione più generale;
escavazione delle stesse o sopraelevazione di pareti
I secondi, cioé quelli a cielo chiuso, sono i più diffusi nel campo acquedottistico e si suddividono in:
- serbatoi interrati
- serbatoi seminterrati;
- serbatoi pensili (o sopraelevati);
I primi sono costruzioni completamente sotterranee, sovente costruite a cielo aperto e poi re interrati, altre volte costruiti in galleria.
Sono realizzazioni costose alle quali si ricorre quando non é possibile una soluzione seminterrato, in genere per questioni morfologiche o paesaggistiche.
Tralasciando di parlare delle vecchie cisterne, alcune di epoca romana tuttora in esercizio, é il caso di citare un esempio recente: il serbatoio Petrizzi sull’ acquedotto dello Jato, a servizio della città di Palermo, realizzato nei primi anni “80 tramite 5 gallerie.
I serbatoi seminterratoi sono quelli di più frequente realizzazione che si fondano su di un modesto sbancamento che poi vizene di norma colmato dalla struttura del serbatoio sulla quale sarà poi posto un modesto strato di terreno con compiti sia paesagistici, ma soprattutto di isolamento termico.
I serbatoi pensili sono serbatoi la cui camera per lo stoccaggio dell’ acqua é posta diversi metri sopra la superficie orografica locale ed é retta da un sistela di muratura, di pilasti, di pile o di setti a seconda dello aspetto architettonico che si intende dare alla struttura
Sono ovviamente i più costosi e possono essere realizzati solo per volumi relativamente modesti.
Ed essi si ricorre quando l’orografia locale non mette a disposizione, cioé nella vicinanze della zona da seevire, idonnee colline sulle quali realizzare serbatoi seminterrati.
Sempre dal punto di vista, possiamo distinguere i serbatoi anche tenendo conto del tipo di materiali con i quali andiamo a realizzarli, avremo:
- serbatoi in muratura;
- serbatoi in calcestruzzo armato
- serbatoi in c.a.p. in opera
- serbatoi in c.a.p. parzialmente prefabbricati;
- serbatoi in acciaio
I serbatoi acquedottistici
Sono depositl dove viene accumulata l’acqua nei periodi in cui la sua produzione (intesa nella accezione più generale ) supera il fabbisogno e dal quale viene prelevata quando si ribalta il rapporto produzione/fabbisogno.
Si definisce periodo di compenso o caratteristico di un serbatoio il più piccolo degli intervalli di tempo per il quale si verifica la
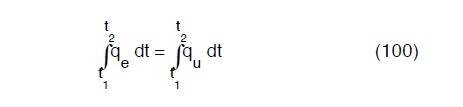
e nello stesso periodo si abbia uno svaso ed un invaso completo della sua capacità utile, definendo con quest’ultimo termine il volume di acqua che può essere immagazzinato tra la quota di minimo invaso (che é la più piccola delle quote possibili per le quali si abbia ancora condotta di uscita in pressione) e la
minima quota di intervento dello scarico di troppo pieno.
In funzione del suddetto periodo possiamo avere serbatoi a compenso:
- giornaliero,
- settimanale,
- mensile,
- stagionale,
- annuale.
In genere per gli acquedotti il periodo di compenso (ciclo caratteristico) é giornaliero o settimanale, ma non sono esclusi altri periodi.
E’ bene però precisare subito che i serbatoi con compensi mensili stagionali od annuali richiedono di norma capacità talmente elevate ( milioni di metri cubi) che diventano dei veri e propri laghi artificiali, realizzabili sbarrando, mediante dighe dei corsi d’acqua naturali.
Più sovente, invece, i serbatoi per acquedotti sono delle vasche, di capacità utile di qualche migliaio di mc, che possono essere contenuto in appositi edifici.
Oltre al suddetto scopo di compenso (giornaliero o settimanale) i serbatoi assolvono anche al compito di riserva, cioè di accumulare una certa quantità d’acqua, oltre quella strettamente necessaria al compenso, da utilizzarsi in casi di emergenza, come la momentanea produzione di acqua o la maggiore richiesta dovuta alla messa in funzione degli idranti.
Un’ altra clasificazione che non si basa sul ciclo caratteristico é funzione di elementi costruttivi quali la posizione dello stesso rispetto al plano di campagna.
Da questo punto di vista, come detto, si classificano in:
- serbatoi interrati;
- serbatoi seminterrati,
- serbatoi pensili
I primi ed i secondi sono caratterizzati dall’avere la base dei serbatoi poggianti direttamente sul terreno, mentre nei serbatoitoi pensili la camera dell’ acqua é a diversi metri ( a volte decine) da piano di campagna.
La differenza trai serbatoi interrati o quelli seminterrati non é netta.
In generale i primi sono realizzati integralmente nel sottosuolo (a volte tramite gallerie) e quindi con modeste o nulle alterazioni del soprassuolo
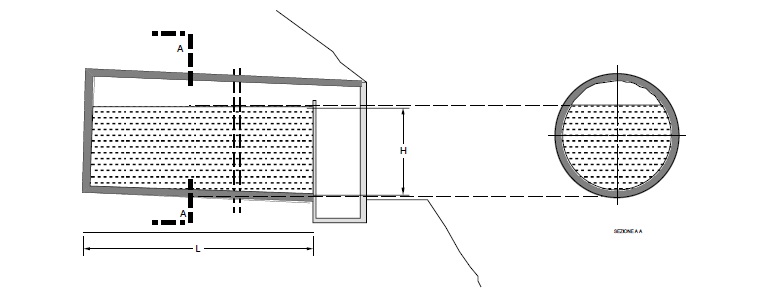
I secondi sono realizzati in genere a “mezza costa” ripristinando poi secondo certe regole il terreno sopra la copertura del serbatoio.
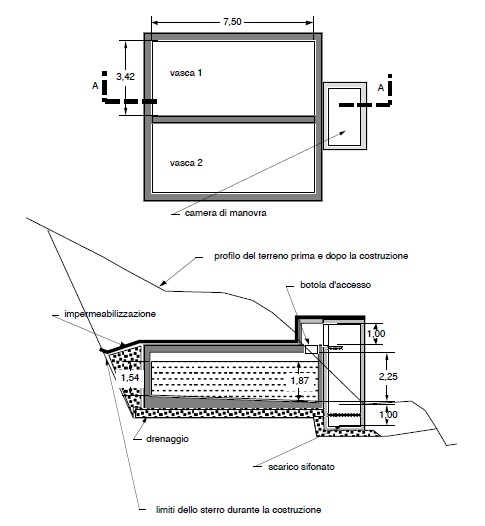
La tendenza a realizzare i serbatoi quando è possibile interrati o seminterrati è legata alla necessità di proteggere l’acqua dalle escursioni termiche dell’ ambiente esterno, è infatti noto che le escursioni termiche del terreno sono strettamente più contenute. Per lo stesso motivo i serbatoi seminterrati vengono o coperti con rilevati artificiali di terra oppure viene realizzata una intercapedine tra la camera d’acqua e
la copertura più esterna. Stesso accorgimento della intercapedine e utilizzato per i serbatoi pensili.
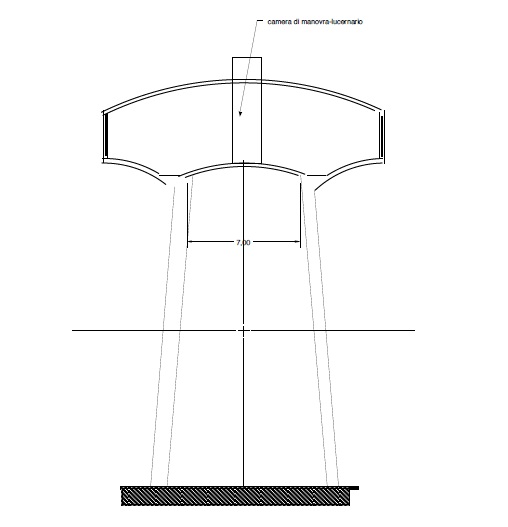
A questi ultimi si ricorre quando si desidera realizzare una alimentazione della rete idrica a gravità e non esistono nella zona rilievi topografici tali da consentire la realizzazione di serbatoi di altro tipo.
Ovviamente i serbatoi pensili sono molto più costosi.La figura che precede illustra uno schema classico di serbatoio pensile (schema Intze).
Dimensionamento volumetrico
Si è già accennato che a seconda del periodo caratteristico si possono avere serbatoi a compenso giornaliero, settimana
Maggiore è il tempo caratteristico, maggiore è in generale il volume che deve avere il serbatoio.
Il volume minimo da dare ad un serbatoio affinché nel periodo caratteristico t0, t* si abbia compenso è dato dalla somma

dove Wi è definito dai massimi valori positivi e negativi dell’integrale
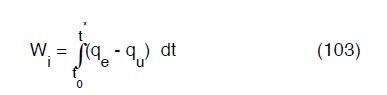
al variare di t nell’lntervallo t0, t*
E’ dunque evidente come, limitatamerte alla sola funzione di compensazione, il volume da assegnare al serbatoio sia funzione delle leggi temporali delle portate entranti e uscenti :

Prima di analizzare le precedenti (104) e quindi di studiare come ottenere gli addendi del secondo membro della (102) precisiamo che la (103) è l’equazione, in forma integrale, di continuità del serbatoio.
Esprime cioè la quantità d’acqua che in un serbatolo si accumula o si svasa nell’intervallo di tempo t0, t*
Più frequentemente della (3) si adotta l’espressione differenziale

detta appunto equazione di contlnuità dei serbatoi od anche equazione dei serbatoi. La (103) si risolve in generale graficamente. Se ci poniamo nel caso più semplice di qe (t) e qu (t) costanti avremo ovviamente l’assenza di qualunque periodo caratteristico e necessariamente
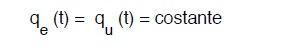
altrimenti se :
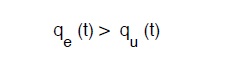
avremo un accumulo sempre crescente di acqua e quindi necessiterebbe un serbatoio infinitamente grande per accumulare istante per istante la portata qe (t) – qu (t). Quantitativo che poi non verrebbe mai utilizzato.
Viceversa quando qe (t) < qu (t) sarebbe necessario ancora un serbatoio infinitamente grande per poter, istante per istante, integrare con (q )u (t) – qe (t) la portata in arrivo. Più frequentemente però la qu (t) è funzione piuttosto variabile del tempo (la qe (t) spesso ha un carattere costante)
Variabllità della portata uscente
In particolare la qu (t) dipende dalla richiesta idrica del centro da servire che varia da istante ad istante, da giorno a giorno, da mese a mese
Si ammette in generale, ed in prima approssimazione che non vari da anno ad anno
La dipendenza della richiesta idrlca è varia, si possono individuare tuttavia quali siano le variabili indipendenti principali:
- la popolazione,
- la temperatura,
- la lavoratività della giornate,
- la contemporaneità d’ uso
Si tenda a quantizzare le variazioni tramite dei coefficienti moltiplicativi [ α , β, δ, ζ ] da applicare al valore medio del periodo di tempo gerarchicamente superiore nella scaletta: anno, mese, settimana, giorno, ora, punta
Di norma la portata media Qm,i del mese i-esimo é dunque data dalla
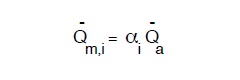
dove, ovviamente:

I valori di αi valutati sulla base di centri tipo si trovano in vari testi e manuali.
Il Ruggiero, ad esempio, dà i valori ripotati nella tabella che segue e che tutt’oggi possiamo ritenere validi per una media città che non abbia particolari migrazioni stagionali di popolazione.
La presenza di migrazioni stagionali può influire moltissimo sui valori di qui quindi αi
Ad esempio in stazioni balneari con forti migrazioni turistiche si presentano nei mesi estivi valori di αi notevolmente superiori a quelli prima indicatiLe stazioni sciistiche ed in generale quelle di montagna, con nei mesi invernali ed in quelli estivi possono presentare due massimi . Esistono poi casi particolari di città con forte popolazione migratoria di universitari che presentano il massimo di richiesta idrica in corrispondenza del periodo degli esami, o di città soggette ad importanti emigrazioni estivo che
possono non presentano il massimo estivo, ecc.
Non esistono sostanziali variazioni sistematiche, in ciascun mese, della portata media settimanale se non che quelle dipendenti dalla temperatura e dal movimento migratorio, già esaminate per le variazioni mensili, pertanto potremo ammettere:
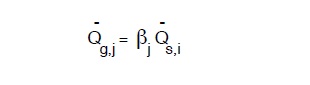
Esistono invece, e sono in genere sistemstiche le variazioni da giorno a giorno della settimana.
Di norma i consumi del sabato e della domenica sono differenti da quelli degli altri giorni vuoi:
a) per la diversa richiesta per usi igienici della popolazione;
b) per le differentl richiesta di eventuali consumi industriali (tra questi
anche gli impianti di condizionomento degli uffici).
Variuazioni analoghe si riscontrano quando si verificano festività lnfrasettimanali ed i relativi “ponti”.
Pur potendo, ovviamento ancora esprimere la portata media giornalieraQ –g,j in funzione della portata media della settimana tramite uno, formula del tipo:
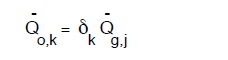
dove:
j è l’ indice del giorno della settimana,
βj il coefficiente moltiplicativo,
Q –s,i è laportata media di una settimana dell’i-esimo mese,
tuttavia tale applicazione è estremamente rara oltre che a causa della imposslbilità
di dare dei valori di βj standardizzati anche per il modesto interesse pratico.
Molto importanti sono, invece le variazioni dei consumi e quindi di richiesta idrica, nelle varie ore della giornata, in generale funzione delle abitudini degli abitantl e della contemporaneità d’uso
Infatti si hanno consumi notturni minimi e massimi al mattino (ora dei lavaggi personali), dalle 12 alle 15 (preparazione dei pasti e lavaggio della casa, delle stoviglie, ecc…), e verso le ore 20 dovuto al lavaggio delle stoviglie della cena, nonché alle pulizie personali.
Si può ancora in generale calcolare le portata media oraria tramite la:
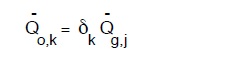
con ovvio significato dei simboli. I valori di δk sono pressocché standardizzati, ma presentano punte maggiori nei centri piccoli.
La tabella che segue riporta i valori di αi e di δk, questi ultimi sono relativi ad una grande città.
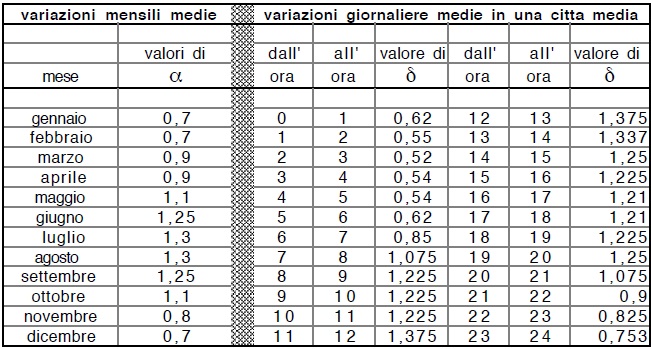
Il valore massimo di δk per piccole città arrirva ad 1,5÷1,6 ed 1,4÷1,5 per città medie.
Anche la portata oraria è pero una portata media, in quanto si verificano, da istante ad istante, differenti richieate d’acqua; non è però possibile, a causa della grande vsriabilità senza regole, dare leggi del tipo delle (7), (8) e (10) per intervalli di tempi inferiori all’ora.
Del resto l’unico interesse pratico è quello di conoscere il valore della massima portata Qmax che in generale si verificherà durante l’ora di massimo consumo orario.
Si ammette in generale che:
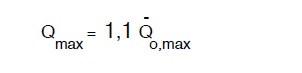
dove
Q –o,max é portata media dell’ora di massimo consumo, che a sua volta, assumendo per δk il massimo di quelli precedentemente tabulati, sarà dato dalla
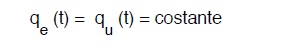
dove
Q –g,max é portata media del giorno di massimo consumo, che a sua volta, assumendo per β il massimo 1,2 sarà dato dalla
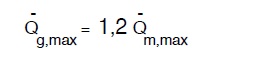
dove
Q –m,max é portata media del mese di massimo consumo, che a sua volta, assumendo per αk
il massimo di quelli precedentemente tabulati, sarà dato dalla
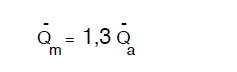
Quindi potremo ricondurre la funzione qu= qu (t) alla funzione:
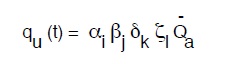
dove αi, βj, δk e ζl sono funzioni temporali che esprimono la dipendenza dal mese, dal giorno, dall’ora, e dall’istante (nell’ora).
Ponendo, per i detti coefficenti, i minimi valori massimi per una città media, cioè :

segue che la portata di punta Qmax sarà data dalla:
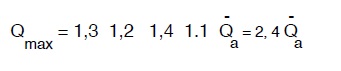
Per centri minori il coefficiente moltiplicatore della Qa può giungere sino a 2,7÷2,9
Variabilità della portata entrante
Le variazioni nelle portate entranti nei serbatoi possono essere dovute a:
a) limitazioni superiori nelle erogazioni dell’acqua da parte delle fonti
di approvvigionamento;
b) manovre di gestione.
Nel primo caso la qe = qe (t) sarà data dalla omonima legge relativa alla fonte di approvvigionamento.
Nel secondo caso la legge è stabillta dall’uomo in funzione della capacità del serbatoio e della qu = qu(t) oltre che dalle disponibilità idriche della o delle fonti di approvvigionamento.
In un successivo sottoparagrafo vedremo come é possibile una tale gestione della legge qu = qu(t).
a) la curva relativa alle portate entranti
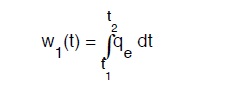
b) la curva relativa alle portate uscenti
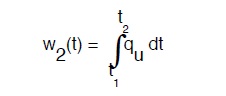
Gli estremi di integrazione, o meglio l’intervallo tra questi estremi, dovrà essere almeno pari o superiore al periodo di compenso.
Quest’ultimo può essere l’incognita del problema postoci (dimensionamento volumetrico) ed in tal caso per determinarlo occorrerà procedere nella costruzione che segue appunto per intervalli sufficientemente
lunghi (a meno che l’esperienza del progettista non sia tale da individuare il periodo di compenso necessario in maniera sintetica da verificare successivamente) oppure potremmo stabilirlo in sede di pre dimensionamento sulla base delle esigenze e delle disponibilità di sito per realizzare il serboatoio.
In generale i serbatoi acquedottistici sono a compenso giornaliero. Stante tale ipotesi dovremo essere in grado di addurre al serbatoio la portata media del giorno di massimo consumo.
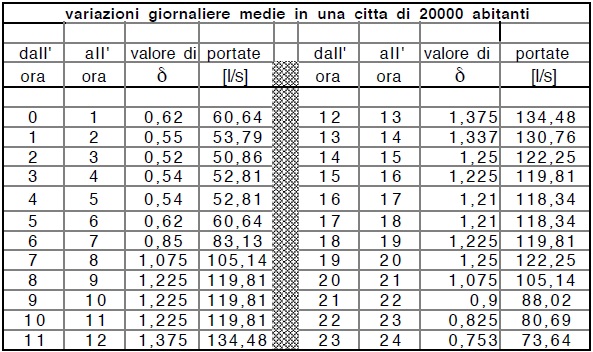
Fissiamo le idee su un centro di 20’000 abitanti, avremo la seguente situazione:

La legge delle portate uscente sarà quella qui di seguito tabulata, e calcolata come visto in precedenza.
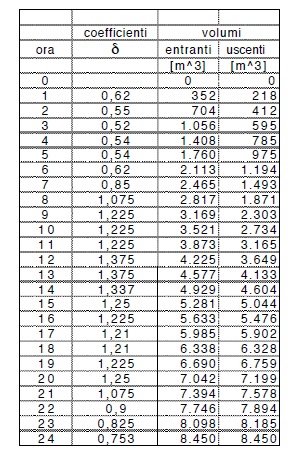
La tabella che segue riporta le curve integrali (a step di un ora) delle qe = qe (t) e della qu = qu (t).
Costruiamo ora il diagramma cui in precedenza.
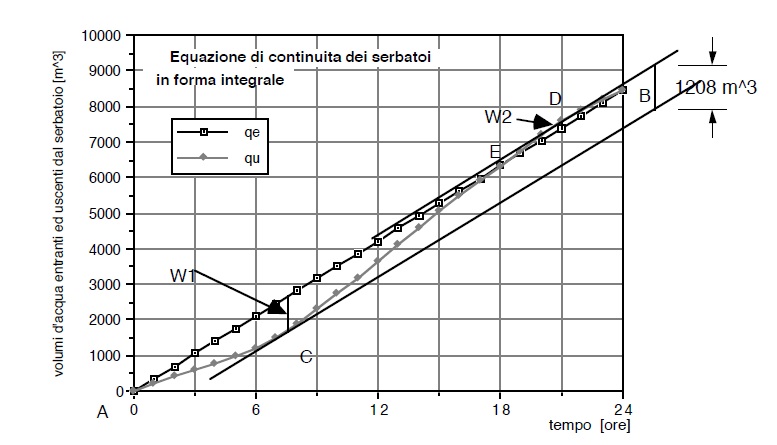
Il segmento verticale che misura la distanza tra le due parallele alla AB l’una per C e l’altra per D rappresenta appunto la somma di W 1 e W 2 e quindi, per la (2) il volume W da assegnare al serbatoio, al fini della dimostrazione della (102) faremo ora l’ipotesi, peraltro non necessaria, ma tuttavia comoda, che l’estremo iniziale di integrazione siano le ore 0,00 del giorno di massimo consumo.
Con riferimento alla figura precedente entreranno volumi d’acqua rappresentati dalle linea marcata da quadratini ed usciranno volumi rapprrsentati dalla linea rappresentata dai rombi.
La differenza, lungo una parallela all’ asse delle ordinate rappresenta, quindi i volumi che si immagazzinano. In particolare nel tratto da A a C avremo prevalenza delle qe rispetto qu (come peraltro é evidente anche dal grafico in quanto la pendenza della curva dell’ integrale delle qe e maggiore di quelle dell’ integrale delle qu). Nel tratto successivo le qu sono maggiori delle qe e pertanto é necessario attinngere al volume immagazzinato. Se supponiamo che il serbatoio alle ore 0,00 iniziali era vuoto, all’ istante corrispondente al punto E sarà stato esaurita la scorta W1 che si era costituita nell’ istante C , ma essendo il serbatoio vuoto per essendovi una richiesta iodrica qu >qe non potrà che essere inviata in distribuzione altro che la portata q e in arrivo. A partire dall’ istante corrispondente al punto D le portate richieste qusono nuovamente minori della qe pertanto si tornezrà ad accumulare acqua nel serbatio.
Alle ore 24 l’acqua accumulata sarà pari al segmento W2 .Il giorno successivo, alle ore 0,00 in serbatoio vi sarà già dunque un volume pari a W2 ed alle ore corrispondenti al punto D il volume totale accumulato sarà pari a W1 e W2 All’ istante E saré stato attinti dall’ acqua immagazzinata un volume pari a W1 e in serbatoio sarà ancora presente un volume pari a W2. Solo all’ istante D verrà consumato anche il volume W2 e quindi il serbatoio sarà vuoto, ma da quell’ istante ricomincia ad accumularsi acqua ed alle 24 avremo nuovamente dispinibile un volume pari a W2 cioé in serbatoio é ormai a regime e pertanto il volume necessario al comenso é esattamente quello indicato dalla (102).
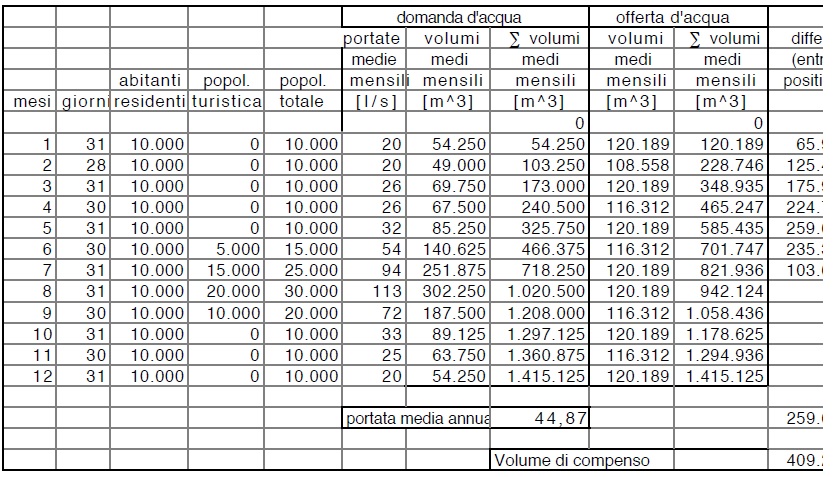
La tabella che segue é la stessa della precedente, completata con il calcolo analitico del volume di compenso.
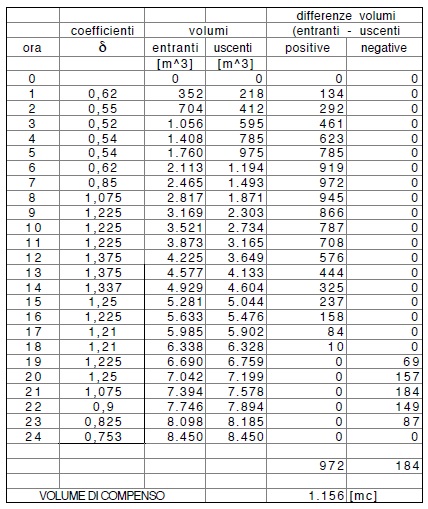
La differenza tra il calcolo grafico é quello analitico é dell’ ordine del 5% (sibadi che il calcolo grafico, qui fatto con computer, così come la tabella-foglio elettronico- potrebbe raggiungere precisioni anche maggiori ma queste non hanno alcun senso pratico. Ovvia la possibilità di invertire le qe e que senza nulla cambiare di avere le due leggi del tutto generiche8 (e non una costante nel tempo come in precedenza supposto).
8L’ equazione di continuità del serbatoio così come in precedenza illustrate hanno valenza molto generale ma con leggi delle qe e delle qu molto diverse a seconda dei casi.
E’ in caso di introdurre a tale punto un dimensionamento di tipo “sintetico dei serbatoi a compenso giornaliero. I calcoli precedenti sono del tutto generici perché redatti con coefficienti validi per città medie. I n tali caso é possibile , senza ricorrere al procedimento (grafico e/o analitico) di risoluzione dell’ equazione di continuità dei serbatoi, dare comunque un dimensionamento agli stessi.
Se dividiamo il volume di compenso, cioè 1156 [m^3], per il volume complessivo d’acqua che perviene al serbatoio nella giornata di massimo consumo, nel nostro caso 8450 [m^3] avremo un numero puro, svincolato dalla portata del giorno di massimo consumo che rappresenta il rapporto suddetto e valido in generale. Quindi detto ψcomp tale rapporto, avremo:

Un caso tipico in cui é ben difficile soddisfare le esigenze con un serbatoio a compenso giornaliero é quello delle località turistiche o con forti migrazioni stagionali, infatti in tali casi ben difficilmente é possibile i nseguire con le portate daaddurre i valori delle portate medie giornaliere richieste.
Se ipotizziamo di addurre solo le portate medie mensili e tenuto conto di un’escursione turistica tale che nei mesi di maggior presenza la popolazione totale si triplichi, avremo dalla risoluzione dell’ equazione di continuità dei serbatoi che sarà necessario un invaso di volume pari a circa il 30% del volume d’acqua che si consuma in un anno. In campo idroelettrico di norme é la qu costante e la qe variabile con il regime fluviale fatte salve le dovute eccezioni sui entrambe le funzioni) In campo irriguo la qe é legata al regime fluviale e/o a modulazioni di serbatoi più a monte mentre la qu é determinata dalla necessità irrigue
Analoghe considerazioni per le altre opere idrauliche.
Per dare un’ idea delle proporzioni, in termini assoluti l’esempio di cui prima porta ad un volume pari a quello di un parallelepipedo che abbia per base il campo di gioco di uno stadio di calcio e per altezza circa 70 metri. Si tratta di volumi enormi che non possono che realizzarsi con invasi artificiali o comunque con vasche all’ aperto.
Volume di riserva
Con tale termine si suole indicare la capacità, aggiuntiva a quella di Compenso ed a quella a disposizione del servizio antincendio, da utilizzare nel caso di interruzione momentanea di servizio delle adduttrici.
L’ordine di grandezza di tale capacità e’ del volume giornaliero d’acqua consumata dal centro da servire.
Pertanto la sua valutazione ha peso nel caso di dimensionamento allorquando di tratta di serbatoi a compenso giornaliero e scarso significato per i serbatoi con tempi di compenso maggiori.
Per la valutazione di tale volume di riserva occorre distinguere a seconda che l’approvvigionamento avvenga da una sola fonte o più fonti e con una o piu’ adduttrici.
Nel caso di più adduttrici, ciascuna proveniente da fonte diversa é piuttosto improbabile che tutte le adduttrici vadano contemporaneamente in avaria pertanto il volume di riserva potrebbe essere inferiore a quella del caso di una sola adduttrice che provenga da una unica fonte di approvvigionamento.
Per tale ultimo caso alcuni Autori segnalano la opportunità che la riserva permetta il prosieguo del servizio delle distributrici per un’intera giornata da quando e’ avvenuto il disservizio della adduttrice e pertanto il volume di riserva dovrebbe essere:
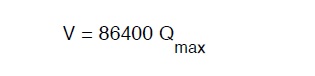
Si ritiene tuttavia che tale volume e’ eccessivo (e’ circa tre volte quello necessario al compenso giornaliero) e pertanto incide fortemente sul costo del serbatoio; altri Autori (Zoccoli – Manuale dell’Ingegnere Civile ed. Cremonese 1981) indicano tale volume di riserva nella metà del precedente cioè:
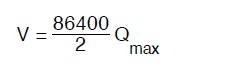
difatto se si tiene conto delle condizioni di emergenza quali quelle di esecuzione dei lavori di riparazione alla fonte di approvvigionamento od alla adduttrice puo’ essere regolata l’acqua in uscita dal serbatoio.
Per esempio, con erogazione non continua ma per turni orari ecc…. si può raggiungere, con costi molto minori, l’ obiettivo di assicurare il servizio idrico per un intero giorno nonostante la mancanza di adduzione al serbatoio. Diverso e’ il caso di una adduttrice che trae alimentazione da più fonti di approvvigionamento; in tal caso il disservizio può essere causa:
a) di riparazione sulla adduttrice;
b) di lavori manutentivi alle fonti di approvvigionamento.
Diverso sarà l’effetto in quanto nella seconda ipotesi l’adduttrice continuerà a funzionare semmai con minore portata.
Tuttavia a titolo prudenziale sarà opportuno dimensionare il serbatoio come già detto per il caso di una adduttrice ad unica fonte di approvvigionamento. Il caso piu’ favorevole e’ quello di diverse adduttrici
Ognuna con fonti diverse di approvvigionamento, in tal caso é improbabile l’avaria contemporanea di tutte la adduttrici.
Pertanto si potrebbe o fare a meno del dimensionamento di riserva o, meglio, ridurre questo alla sola riserva per mezza giornata calcolata sulla base della adduttrice di maggiore portata.
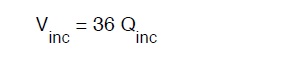
Dove :
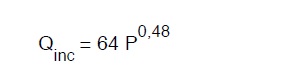
Con

E
P popolazione del centro da servire espresso in migliaia di abitanti. E’ da precisare che tale formula e’ inapplicabile per centri con popolazioni inferiori alle 5000 unita’, in quanto altrimenti porta a sopradimensionamenti.
Considerazioni finali sul dimensionamento idraulico dei serbatoi
Il dimensionamento idraulico, cioé volumetrico dei serbatoi é dato dalla somma dei tre volumi precedentemente determinati:
- volume di compenso,
- volume di riserva
- volume antincendio.
E’ tuttavia da precisare che non sempre é possibile e/o conveniente progettare i serbatoi per la somma dei suddetti tre volumi. Infatti, se soprattutto trattasi di serbatoi pensili, l’onere di costruzione di un
serbatoio di grandi dimensioni puo’ essere tale da consigliare l’adozione di serbatoi a solo compenso giornaliero o poco più.
D’altra parte i volumi si riserva ed antincendio diventano di ordine di grandezza trascurabile se li si confronta con quelli di compenso quando questo sia stagionale od annuale (oggi soluzioni di tale tipo sono sempre piu’ frequenti) pertanto il solo dimensionamento di compenso é di norma in tali casi sufficiente anche per le altre funzioni. E’ anche da notare che il volume come sopra determinato é quello utile, il volume effettivo sarà maggiore di quello utile dovendo aggiungere a tale ultimo quello dell’acqua contenuta tra il fondo delle vasche ed il livello piu’ alto della tubazione di presa. Riprendendo le considerazioni sul dimensionamento sintetico di serbatoi a compenso giornaliero, e tenuto conto che il rapporto

vale 0 ,136 ed aggingendo a questo un modesto volume di riserva ed antincendio, in generale si ammette che:

Considerazioni economiche globali sul dimensionamento idraulico adduttrice-serbatoio (armonizzazione)
Un serbatoio di compenso annuo richiede una capacità rilevante questa si riduce considereviolmente quano il compenso é mensile ed si ruiduce maggiormente per un compenso giornaliero
Ciò comporta che la portata entrante nel serbatoio non dovrà avere la caratteristica della costanza nel tempo , infatti solo per i serbatoi a compenso annuale la portate entrante potrà essere sempre costante alla portata media annua, negli altri casi sarà, ad esempio:

Quindi le tubazioni di adduzione al serbatoio dovranno essre di volta in volta dimensionate per la massima portata che dovranno trasportare.
Si pone dunque un problema di armonizzazione globale che può essre rappresentato come segue.
1) premesso che ovviamente il costo di costruzione del serbatoio sarà tanto maggiore quanto lo sarà la sua capacità utile e pertanto quanto maggiore é il suo periodo caratteristico di compenso;
2) premesso che ovviamente il costo di costruzione della addutrice sarà tanto maggiore quanto lo sarà la portata massima che dovrà trasportare e pertanto quanto minore é il periodo caratteristico di compenso del serbatoio;
converrà:
realizzare un serbatoio grande ed una adduttrice di piccolo
diametro o viceversa?
Il problema fu affrontato e risolto dal Conti9 Innanzi tutto occorre esprimete in termini analitici il costo di costruzione del serbatoio. Di certo esso sarà proporzionale (in modo pressocché lineare) al volume della struttura delle vasche, che a sua volta sarà proporzionale alla capacità utile, dunque si può ammettere che si abbia:

dove:
Cunit é il costo del serbatoio d’acquedotto a m^3 di volume utile
Si definiscono ora due rapporti:
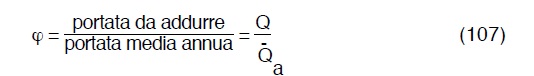

sostituendo la (108) nella (106) avremo:
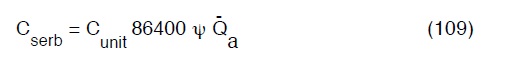
pertanto il costo totale dell’opera sarà:
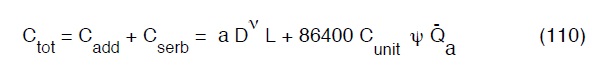
che dovrà essere minimizzato.
Il Conti, confrontando i dati di un considerevole numero di città é riuscito ad individuare seppur per punti la legge ϕ = (ψ) che lega quindi portata da addurre a volume del serbatoio.
9 Conti Luciano (1868-1940) tra i massimi acquedottisti italiani. Fu professore di Costruzioni Idrauliche dal 1913 al 1938 prima a Padova, poi a Pisa e quindi a Roma.
Notevoli sono i suoi scritti in campo acquedottistico, purtoppo rarissime sono le copie degli stessi.
I punti sperimentali del Conti sono quelli della tabella che segue.
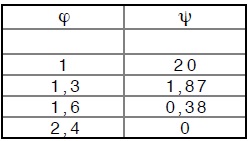
La cui riduzione grafica é qui di seguito riportata.

Detto Y il carico idraulico disponibile tra fonte di approvvigionamento e serbatoio, sarà ovviamente, dalla (59) :

dalla quale avremo:

tenuto conto della (107) avremo:
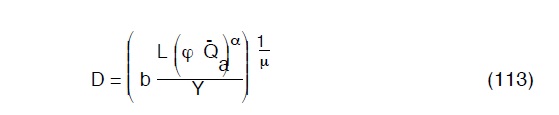
che sostituita nella (110) da:
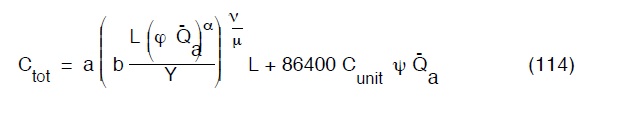
La condizione di minimo costo sarà ovviamente espressa dalla:

segue
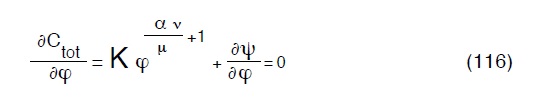
dove si é posto
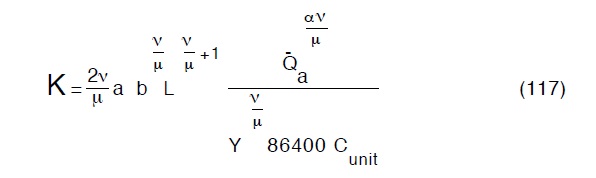
La (116) in forma logaritmica diventa:
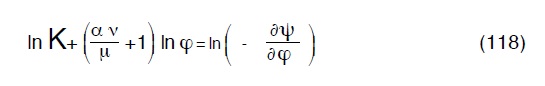
che rappresenta una retta di ordinata all’origine pari al n K e coefficiente angolare
parli a ![]()

è positivo essendo ψ decrescente con ϕ.
La risoluzione della precedente non é immediata. Qui di seguito diamo un procedimento grafico, ideato sempre dal Conti per la sua soluzione, ovviamente oggi sono possibili metodo numerici ma il metodo grafico ha ancora tutta la sua attualità non soltanto per l’elaganza ma anche perché rimane ancora uno dei mezzi più spediti soprattutto se si ricorre all’ uso di fogli elettronici e di grafica computerizzata.
La soluzione della (118) altro non é che la ricerca dell’ intersezione in un piano cartesiano che abbia:

della retta di equazione (118) con la curva che che rappresenta
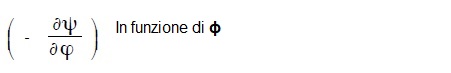
Fissiamo l’attenzione su un esempio concreto. Si abbiano dunque i dati della seguente tabella:
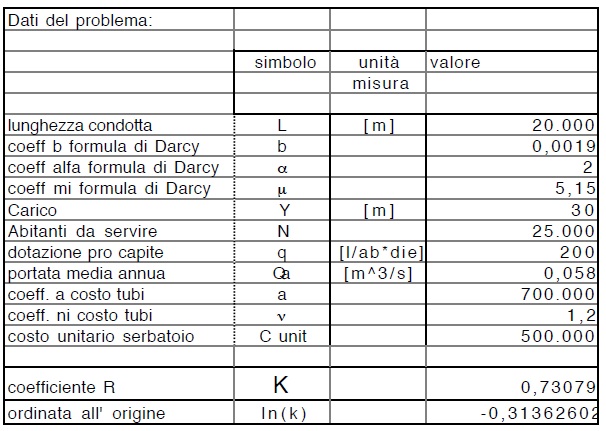
Dalla precedente é possibile calcolare alcuni punti della retta (118), come riportato nella tabella che segue
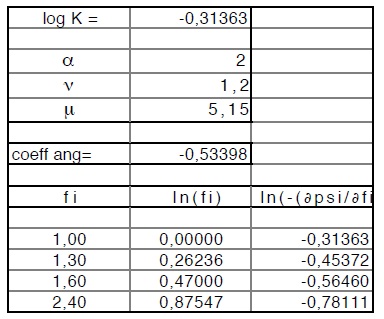
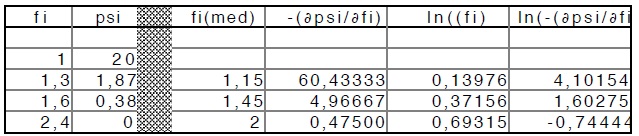
Nel contempo la tabella seguente da la determinazione di tre punti della curva delle ln

in funzione di log (ϕ):
Riportando i punti delle due ultime tabelle in un diagramma, avremo una figura del tipo di quella qui di seguito rappresentata
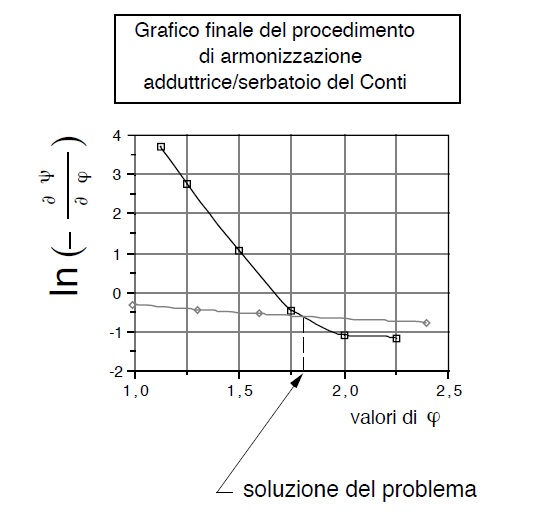
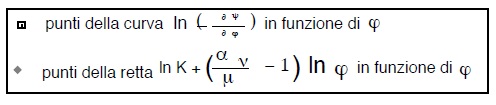
Oltre al citato e classico procedimento del Conti per l’armonizzazione tra condotta addutrice e serbatoio neesistono altri che si differenzuano dal primo per le diversità delle situazioni particolari trattate.
Qui accenniamo solo ad un metodo di armonizzazione globale del Mantica (L’Ingegnere, 1975) riferito a casi in cui sia presente il sollevamento meccanico e pertanto nel computo gobale dei ciosti sono presenti anche quelli di sollevamento.
In tali casi può essere conveniente studiare, dal punto di vista economico, anche la posizione altimetrica del serbatoio.
