
Con il termine adduzione si intende il trasporto dell’acqua dalle opere di captazione alla (od alle) località di utilizzazione (cioè di distribuzione).
Il collegamento con la rete distributiva, e con le opere di captazione, può essere diretto o con interposizione di serbatoio a seconda di varie condizioni che verranno esaminate nel capitolo dedicato ai serbatoi.
Le opere di adduzione, come quelle di distribuzione sono dette condotte o condutture.
Una prima distinzione nelle opere di adduzione fatte esclusivamente in base ad un criterio idraulico di grande importanza nella definizione progettuale e realizzativa del suo profilo altimetrico è quella di suddividerle in:
- condotte in pressione
ed in
- condotte a pelo libero.
Altra importante distinzione è basata sul tipo di energia necessaria al trasporto dell’acqua. Da questo punto di vista si suole suddividere le adduttrici in: - adduttrici a gravità
ed - adduttrici a sollevamento meccanico.
Per la prima l’energia motrice è fornita dal peso proprio dell’acqua.
Chiaramente un tale schema è possibile solo quando esiste una differenza di quota tra la posizione di partenza e quella di arrivo dell’acqua.
Per la prima l’energia motrice è fornita dal peso proprio dell’acqua.
Chiaramente un tale schema è possibile solo quando esiste una differenza di quota tra la posizione di partenza e quella di arrivo dell’acqua.
E’ ancora da dire che detta differenza di quota deve essere sufficiente a far vincere la resistenza che incontra l’acqua nel passare per la adduttrice nella quantità d’acqua voluta. Nel secondo caso questo dislivello o è troppo piccolo o non esiste od addirittura può essere negativo (quando la posizione di partenza è più bassa di quella d’arrivo). Sarà allora necessario conferire all’acqua l’energia occorrente per il
movimento tramite organi meccanici.Di norma pompe centrifughe. I locali che ospitano le pompe ed i loro accessori sono detti stazioni o centrali di spinta e di essi ci occuperemo in altra sede
Evidentemente le condotte a pelo libero sono compatibili solo nel caso di adduttrici a gravità.
Gli acquedotti del passato erano realizzati a pelo libero dapprima per l’indisponibilità di materiale atto a realizzare tubazioni in pressione e più recentemente per la maggiore convenienza economica del pelo libero rispetto ai tubi di ghisa ottenuti per fusione prima della “rivoluzione industriale”. L’avvento dei procedimenti industriali per la costruzione dei tubi ha portato come diretta conseguenza il proliferare degli acquedotti e la sostituzione quasi completa dello schema a pelo li bero con quello in pressione. Sono rimaste solo pochissime adduttrici a pelo libero ma ciò spesso è stato dovuto a motivi storicoartistici
e/o legali che a motivi tecnici . Ciò non toglie che tuttora, o per ragioni tecniche od economiche lo
richiedano, possono realizzarsi tratti o addirittura l’intera adduttrice a pelo libero. Da un punto di vista puramente idraulico a parità di portata le perdite di carico sono più forti per le condotte in pressione (almeno con tubazioni tradizionali) che per condotte a pelo libero a piccola pendenza a sezione circolare
chiusa che abbiano il medesimo diametro con altezza di riempimento pari a quella corrispondente alla portata massima. Ma questa condizione non è certo sufficiente a far preferire le condotte a pelo libero a causa delle difficoltà che si incontrano nell’attraversamento di terreni non pianeggianti e, l’impossibilità di eseguire, poi non solo in termini di corretta economia, variazioni (nel senso di aumenti) della portata da trasportare. Inoltre oggi, il vantaggio idrico cui dianzi si accennava, è scomparso a causa della diminuita scabrezza delle pareti interne dei moderni tubi per acquedotto. Per motivi igienici è inoltre opportuno che gli acquedotti a pelo libero siano sempre a sezione chiusa.
Il Tracciato
Il tracciato degli acquedotti, sia in pressione che a pelo libero va studiato con gli stessi metodi della progettazione delle strade. Ciò comporta, come ovvia conseguenza, che buona parte de gli acquedotti scorre al di sotto di strade rotabili o le fiancheggia.
E’ tuttavia da notare subito che tale soluzione non è soltanto frutto dellamedesima tecnica progettuale ma anche di altri motivi (tecnici, economici e legali) quali la possibilità di evitare o quanto meno ridurre le espropriazioni o comunque le servitù da imporre per l’attraversamento di terreni privati con acquedotti.
Il tracciato va quindi studiato su una carta a curve di livello (ma parallelamente anche sulle mappe catastali) con le stesse tecniche dello studio di un tracciato stradale, tenuto presente che:
a) la larghezza della striscia di terreno interessata dall’acquedotto è in genere molto limitata. Da 80 cm a qualche metro (ma per diametri molto grandi).
b) le tubazioni in genere sono interrate.
c) Esistono delle notevoli limitazioni e alle quote in sé ed alle pendenze del profilo longitudinale dell’acquedotto.
Il tracciato degli acquedotti a pelo libero
Queste limitazioni sono più forti per gli acquedotti a pelo libero in quanto la pendenza piezometrica della condotta libera non deve mai essere positiva cioè deve sempre verificarsi che:

con
z quota del pelo libero su un orizzontale di riferimento,
s ascissa curvilinea verso positivo equiverso con quello di flusso.
Tale ovvia limitazione comporta una meno forte, ma comunque sempre notevole, limitazione sulle pendenze di fondo del canale e ciò in quanto è molto ridotta la possibilità di scambio tra l’energia di posizione e quella di pressione (essendo, quest’ultima, al pe lo libero pari a quella atmosferica). Possono presentarsi quindi le seguenti difficoltà:
a) oltrepassare un rilievo,
b) oltrepassare una depressione ovviamente quando non è possibile aggirarli o, se tale possibili tà esiste, non è economicamente e tecnicamente valida.
Il primo di tali casi, l’oltrepassamento del rilievo, può venire effettuato, a seconda dell’entità del rilievo al di sopra della livelletta dell’acquedotto, della natura del terreno e di eventua li insediamenti sul rilievo stesso, o con trinceeo con gallerie.
Il primo caso, comunque non differisce sostanzialmente dal normale scavo per la posa in opera dell’acquedotto salvo che per le dimensioni. Le gallerie sono invece simili a quelle stradali ed è opportuno che in esse vi alloggino non solo le tubazioni ma si faccia anche posto per un camminamento di ispezione.
Il secondo caso, oltrepasso di una depressione, può essere affrontato:
a) con ponti-canali
b) con inserzione di un tratto di condotta in pressione (questo metodo è detto comunemente, sebbene impropriamente, sifone).
I ponti canali sono normali ponti, e quindi strutture da progettarsi e calcolarsi con la usuale metodologia della scienza e tecnica delle Costruzioni, che in luogo della sede stradale hanno un canale fiancheggiato da uno (o da entrambi i lati) da una passerella pedonale chiusa al pubblico ma che servirà per ispezioni e lavori di pulizia e manutenzione del ponte e del canale. Il sifone è in genere più economico e consiste nel realizzare tra due tratti a pelo libero un tratto in pressione. L’interfaccia tra i due tipi di condotta è
caratterizzata dalle opere di imbocco e sbocco
Le prime sono più complesse dovendo ospitare oltre ad una griglia ed agli organi di interclusione, anche degli sfioratori in modo da regolare la massima portata che può passare attraverso il sifone. Il tratto più depresso da oltrepassare sarà in genere un corso d’acqua e qui per il sifone si presentera la medesima
problematica che per le condotte in pressione alle quali si rimanda.Nel complesso l’attraversamento di una depressione con un sifone si realizza secondo il profilo schematico seguente.
Il tracciato delle condotte in pressione
Per le condotte in pressione non sussistono limitazioni circa il valore della
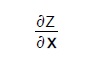
bensì solo limitazioni su ζ asse della condotta
In particolare, deve essere verificata la
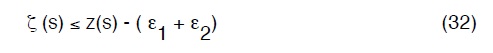
Dove :

ed

E’ ovvio che la (32) è meno limitativa della (31).
Pertanto, sempre nel rispetto della (32), è in genere possibile far superare ad una tubazione in pressione anche dei rilievi senza peraltro dover ricorrere a gallerie o trincee, semmai approfondendo gli scavi che da 1÷1.5 metri normali possono arrivare sino a 3 metri (anche 4 eccezionalmente).
Le difficoltà che si presentano per i tubi in pressione sono relative:
- all’attraversamento di corsi d’acqua
- all’attraversamento di ferrovie.
Un corso d’acqua può essere attraversato tramite:
1) l’utilizzo della struttura di un ponte stradale;
2) la realizzazione di una passerella che regga il tubo;
3) la realizzazione di un tubo autoportante;
4) la semplice posa in opera del tubo al di sotto dell’al veo fluviale;
5) la realizzazione di briglie o soglie;
6) una galleria.
Vediamo separatamente i vari sistemi.
Se esiste un ponte stradale e l’ente proprietario del ponte (Anas, Province, Comuni, consorzi, ecc.) e la struttura stessa del ponte acconsentono sarà possibile collocare il tubo o all’interno della stessa struttura del ponte (ponti a cassone) o appoggiarlo ad esso tramite mensole o organi del genere. Il più frequente ed il più interessante tipo di attraversamento ferroviario è quello interrato.
Questo si realizza, in genere, con la cosiddetta macchina spingitubo; infatti fissata la posizione (nel profilo longitudinale della ferrovia) di attraversamento si posiziona il tubo di protezione e si scava al suo interno, con apposita macchina che automaticamente, con l’avanzare dello scavo, fa avanzare anche il tubo.
Posizionato così il tubo di protezione viene poi inserito il vero e proprio tubo acquedottistico.
Gli schemi d’adduzione
Indichiamo con schemi di adduzione la distinzione tra condotte semplici e condotte ramificate.
Avremo:
a) le condotte semplici sono quelle che riforniscono un sol centro e non distribuiscono acque lungo il percorso. Si porta ad esempio l’acquedotto di Livorno, che trael’acqua dalla falda del subalveo del fiume
Serchio e con una adduttrice di ben 20 Km (ø 800 in fibrocemento) adduce l’acqua ad un serbatoio interrato nella città;
b) le condotte con variazioni di portata lungo il percorso sono quelle che pur avendo come principale obbiettivo il rifornimento idrico di un sol centro, assolvono altresì, lungo il percorso, a compiti distributrici. Un tempo tale tipo di adduzione era frequente, ma oggi è in disuso in quanto l’erogazione lungo il percorso penalizza fortemente ed in modo incontrollabile la portata che perviene alla estremità, cioè al centro da servire. Si cita, come esempio, la vecchia adduttrice di Pisa a Marina di Pisa,che alimentava tutte le frazioni sparse lungo i 12 Km del suo percorso.
Questa condotta è stata poi sollevata dai compiti adduttrici e ora assolve solo compiti distributrici.
c) Le condotte consortili o con diramazioni sono quelle (senza distribuzione lungo il percorso) che assolvono al compito di rifornire più centri: la figura seguente dà lo schema dell’acquedotto del Giardino, un
importante acquedotto a schema consortile,realizzato dalla Cassa del Mezzogiorno in Abruzzo che rifornisce numerosi centri (tra cui Chieti e Pescara).
d) Condotte consortili con variazioni di portata anche nei singoli tratti il nome indica già la funzione di tali adduzioni, anch’esse – come quelle alla lettera b, ormai in disuso, almeno come pratica progettuale e realizzativa, ma ovviamente tuttora in esercizio dove esistono. Si cita come esempio l’acquedotto del Tavo (Abruzzo). La figura seguente ne illustra un tratto con le sue numerose diramazioni.
e) Reti di adduzione. Con questo nome indichiamo non condotte o adduttrici singole, ma un complesso di condotte, tra loro interconnesse che adducono acqua ad uno o più centri. Un tempo una tale soluzione
era da considerarsi atipica e da evitarsi a càusa delle difficoltà di gestione e di manutenzio ne.
Oggi invece, per vari motivi è diventato unsistema molto interessante proprio perchè permette di “gestire” l’adduzione soprattutto quando l’acquedotto (o gli acquedotti) traggono alimentazione da falde; infatti in questo modo è possibile favorire la ricarica di una falda e sfruttarne altre ecc. disinserire una alimentazione se risultasse inquinata o ancora approvvigionare in modo diverso i centri nel caso che una adduttrice sia fuori servizio per lavori di manutenzione (siano essi voluti che dovuti a guasti o rotture) evitando di lasciarli all’asciutto. Come esempio di reti di adduzione citiamo quello di Pisa e Livorno (e centri limitrofi minori)
che in funzione da una decina di anni ha dato ottimi risultati tecnici. La figura seguente ne mostra uno schema semplificato, in esse sono indicati con F i punti di alimentazione possibili degli acquedotti e con S i serbatoi. Nel caso specifico delle città toscane la rete permette di privilegiare Livorno, Marina di Pisa e S. Giuliano Terme nei mesi estivi (che hanno per turismo maggior numero di abitanti), ed in quelli invernali
Pisa che è invece gravata dagli studenti.
Elementi sul costo delle condotte.
Ogni dimensionamento di opere d’ingegneria non può prescindere da considerazioni economiche, cioè dai costi di realizzazione dell’opera e da quelli di gestione.ciò vale ovviamente anche per le condotte in pressione I costi di costruzione, almeno relativamente alla sola condotta adduttrice sono ovviamente:
a) oneri di espropriazione (eventuale);
b) scavo a sezione obbligata e ristretta;
c) costruzione della condotta (inclusa fornitura e posa in opera di tubi, pezzi speciali ed apparecchiature, preparazione del letto di posa,realizzazione di pozzetti, ecc.
d) reinterro con materiale arido;
e) ripristino della pavimentazione stradale (eventualmente).
Di tali voci la a), la b), la d) e la e) sono pressocchè invariabili al variare del diametro (ed eventualmente, e dentro certi limiti, del materiale). Variabile e notevolmente è invece la voce c). Quest’ultima peraltro si compone ancora di vari elementi ma quello che la compone quasi totalmente (circa il 90%) è il costo della tubazione. Detto costo è ovviamente proporzionale alla quantità di materia le (peso) che costituisce un metro di tubo.
Per una prefissata pressione nominale p del tubo con cui costruire l’acquedotto, se la parete del suddetto tubo è sufficientemente piccola nei confronti del diametro, si può supporre che, una volta questo sezionato come i nella figura seguente, la forza T che tiene unito il tubo è esprimibile tramite la:
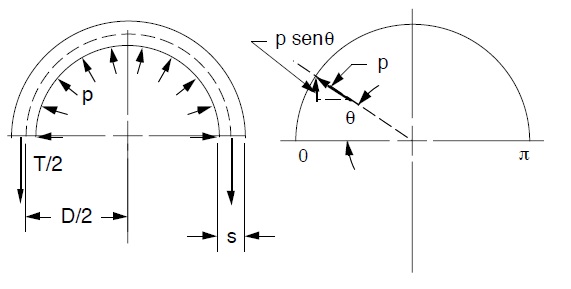
dove:
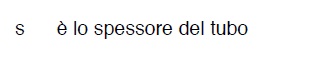
e

supposta costante (o per lo meno poco variabile) nello spessore Imponendo l’equilibrio avremo:
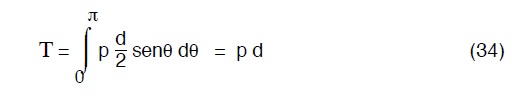
confrontando la (33) con la (34) segue la nota formula di Mariotte:

Quindi lo spessore minimo per il tubo si ottiene dalla (35) ponendo al posto di σ la tensione ammissibile σamm cioè:
Lo spessore reale lo si ottiene aggiungendo ad s uno spessore di sicurezza.s0
Pertanto detto spessore sarà:

L’area di materiale nella sezione (e quindi il suo valore per un metro di tubo) sarà (in termini approssimati ma significativi):
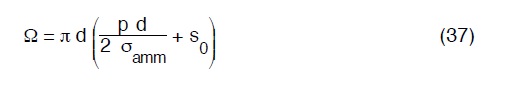
e quindi
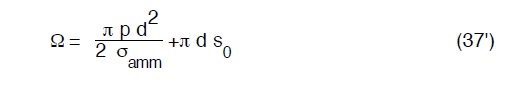
Il peso P di un metro di tubo si otterrà moltiplicando il volume della (37′) per il peso specifico γt del materiale, segue:

dove a e b sono due coefficienti funzioni della tensione ammissibile, dello spessore s0, del peso specifico γt e della pressione di esercizio
Detto quindi c il costo del materiale del tubo per unità di peso segue che il costo C di un metro di condotta può essere espresso dalla:

Doce a’ e b’ sono gli analoghi di a e b moltiplicati per c. Per i calcoli di cui nel seguito la (39) si presta male e sovente in suo luogo si adopera la formula monomia

che se ben valutati α e ν approssima in modo soddisfacente la (39). In forma logaritmica la (40) si t rasforma in una retta.Pertanto disponendo, ad esempio di un listino prezzi, dei costi per i varidiametri sarà possibile da un grafico su scala bilogaritmica valutare α (ordinata all’origine) e ν coefficiente angolare.
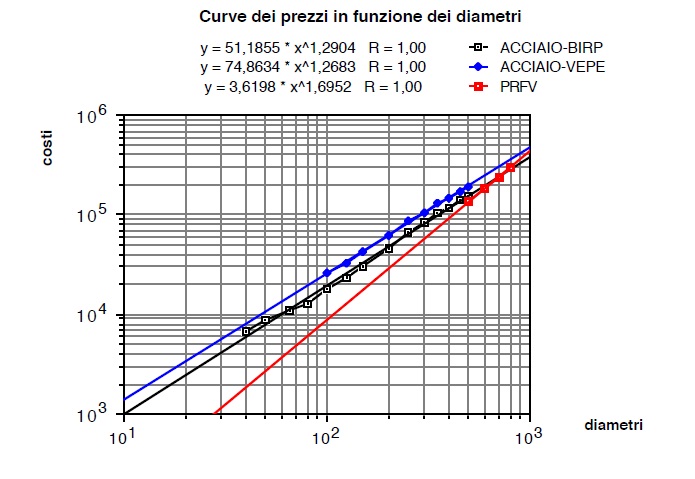
Il precedente grafico é tratto da prezzi di listino del 1993 ed é relativo ai
seguenti materiali:
- tubi in acciaio con rivestimento bituminoso pesante (ACCIAIO-BIRP)
- tubi in acciaio con rivestimento esterno in PEAD ed interno in resina
epossidica (ACCIAIO-VEPE) - PRFV centrifugato rigidezza 10’000 N/m2
L’idraulica delle adduttrici in pressione
L’idraulica delle adduttrici in pressione è l’idraulica delle lunghe condotte (in pressione), si ritengono cioè trascurabili le perdite di carico localizzate dovute a gomiti e curve in generale, allagamenti o restrizioni di sezione, ecc… in quanto la loro entità globale è trascurabile rispetto a quella delle perdite di carico distribuite. Il tipo di moto è in generale turbolento , cioè con Re>100.000
Queste ultime possono, per il moto uniforme, essere valutate con varie formule che però le possiamo in generale ricondurre alla vecchia formula di Darcy-Weisbach

con ovvio significato deio simboli, sostitendo a

segue la

da cui

posto quindi

segue infine

che è la classica formula di Darcy
Esplicitando invece la (40) in v avremo

da cui, tenuto conto che Rm=d/4 avremo:

e quindi:

ponendo dunque:

infine avremo

che é la ben nota formula di Chezy dove il coefficiente X può essere valutato e per mezzo delle formule di Bazin

o con quella, semplificata, di Kutter

Il valore di λ può essere ancora ottenuto dalla
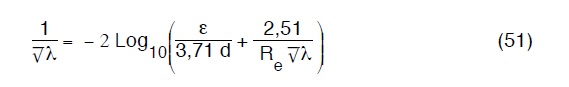
che è la ben nota formula di White-Colebrook. Quest’ultima è molto più generale delle precedenti in quanto vale anche per i moti di transizione cioè con numeri di Reynolds molto bassi (comunque superiori ai 3500).
Affianco all’ espressione White-Colebrook ne convivono altre ed in particolare dovute a:
Nikuradse
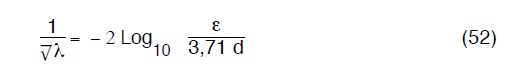

Von Karman
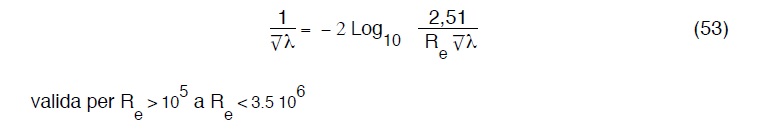
Blasius

E’ da precisare che queste formule che a prima vista possono sembrare più precise di fatto possono essere causa anche di errori maggiori in quanto la presunta loro maggiore precisione può essere inficiata dalle maggiori difficoltà di utilizzo (valutazione di Re per successive iterazioni) e da scelte più difficili relative alla scabrezza relativa ε/d
Molti importanti idraulici ( Di Ricco, Altschoul, Supino, Citrini, Curto e più recentemente anche Vitale e Mancinelli) sono stati affascinati dalle formule di Collebrook e consimili ed ne hanno proposto formulazioni più o meno esplicite che ne semplificassero l’utilizzo, ma tutte hanno avuto scarso seguito
Parallelamente a questa vengono adottate altre formule di tipo monomio, tutte riconducibili alla formula di Manning

analoga alla precedente é la di Gaukler o di Strickler

Ne segue ovviamente che:

Prima di affrontare l’argomento dei coefficienti di scabrezza non è forse inutile ricordare che ancora molti uffici tecnici degli enti pubblici italiani richiedono per la valutazione della perdita di carico la formula impropriamente detta di Bazin-Fantoli:
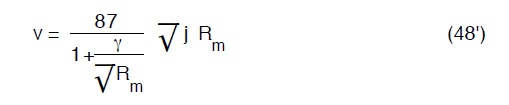
che altro non è, in effetti, che la formula di Chezy con χ di Bazin.
Il nome dell’idraulico italiano Fantoli è stato aggiunto perchè questi indicò i valori di γ da adottare per i tubi allora in uso (acciaio, ghisa).
La classica formula di Darcy (45) a rigore è valida solo per tubi in ghisa. Per la ghisa nuova il coefficiente β da adottare é dato dalla:
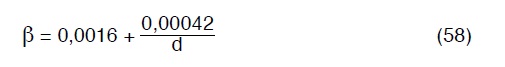
per la ghisa usata si adotta un coefficiente β pari al doppio di quello calcolato tramite la (58).
A causa della presenza di d nel secondo membro della (58), la (45) non ha forma monomia, tuttavia essa è riconducibile, con buona approssimazione alla seguente detta anche di Darcy-Contessini:

dove b, α e μ venbgono fissati in funzione del tipo di materiale e del relativo stato di usura.
La tabella che segue ne riporta taluni valori.
| MATERIALE | b | α | μ |
| ghisa lamellare nuovi | 2 | 5 | |
| ghisa lamellare usata | 2 | 5 | |
| ghisa sferoidale e/o rivestita | ,0019 | 2 | 4,9 |
| acciaio nuovo | ,0016 | 1,85 | 5,32 |
| acciaio in esercizio | ,0019 | 1,85 | 5,32 |
| fibrocemento | ,0025 | 1,785 | 4,785 |
| PRFV, PVC, PEAD | ,0006 | 2 | 4,7 |
Anche la formula di Chezy e quella di Strickler sono molto usate, qui nel seguito si riportani i relativi coefficienti (tratti dal manuale dell’ Ingegnere Civile edizioni Cremonese-1981)
| MATERIALE | Bazin [m1/2] | Kutter [m1/2] | scabr eq. [mm] | Stickler [m1/2s-1] |
| ghisa lamellare nuovi | 0,1 | 0,15 | 0,2-0,4 | 100 |
| ghisa lamellare usati | 0,23 | 0,35 | 1÷2 | 75÷70 |
| ghisa sferoidale e/o rivestita | 0,06 | 0,12 | 0,1 | 105 |
| acciaio nuovo | 0,005 | 0,12 | 0,05 | 120 |
| acciaio in esercizio | 0,1 | 0,16 | 0,2÷0,4 | 90 |
| fibrocemento | 0,23 | 0,35 | 2 | 70 |
| PRFV, PVC, PEAD | 0,04 | 0,1 | 0,04 | 140 |
Si è già avuto modo di notare si è fatta una distinzione tra tubi nuovi e tubiusati (od in servizio).
Questa distinzione, peraltro non esaustiva, trae origine dal fatto che i tubi in specie quelli metallici non internamente rivestiti, una volta postl in opera ed in esercizio sono soggetti ad invecchiamento che consiste nell’aumento della scabrezza delle pareti, a volte nella diminuzione di sezione.
Quelli in materiale plastico, oltre a questo fenomeno, invero più modesto, presentano quello della ovalizzazione che può essre anche estremamente gravi per tubi che:
- o non abbiano sufficiente rigidezza propria;
- o non siano stati bene posti in opera.
Come conseguenza è la diminuzione di portata (a parità di cadente piezometrica).
Le cause di questo fenomeno sono da ricercarsi nella aggressività delle acque e nella disponibilità ad essere aggredito da parte del materiale costituente la condotta.
I materiali più aggredibili sono quelli ferrosi (e questo è il motivo per cui vengono rivestiti) in particolare le acque ricche in ferro-batteri possono provocare gravi tubercolizzazioni ed incrostazioni con asperità relativa dell’ordine dei millimetri ed anche dei centimetri1E’ pertanto necessaria la scelta di una formula, per i calcoli idraulici, che tengaì conto dell’invecchiamento in modo da evitare l’inconveniente che dopo qualche anno dalla realizzazione dell’opera acquedottistica questa adduca portate inferiori. A tal proposito è sempre opportuno eseguire in fase di progettazione calcoli di verifica per le condizioni di tubi in servizio corrente. Contrariamente a quanto si verifica per i canali, nel caso di lunghe condotte in pressione ha poca importanza lo studio del moto permanente in quanto questo si verifica solo localmente in seguito a variazione della sezione del tubo mentre la norma è rappresentata dal moto uniforme. Il moto vario si verificherà ogni qual volta verranno effettuate manovre di apertura o di interclusione sia volute che accidentali. Una trattazione, però, dei fenomeni di moto vario esula dalle intenzioni del presente Capitolo e si rimanda al Cap. II – parte II “Canali e condotte”.
1 Per le condotte adduttrici in ghisa realizzate nel 1911 e da allora in esercizio sono stati effettuati dal Mantica (1972) alcuni controlli tramite la formula di Withe-Collebrook, né é risultato una scabrezza effettiva pari a 9 mm
Condotta in materiale prefissato congiungente due serbatoi
senza erogazione lungo il percorso.
E’ il caso più semplice di condotta adduttrice, la cadente piezometrica è fissata dai due serbatoi.
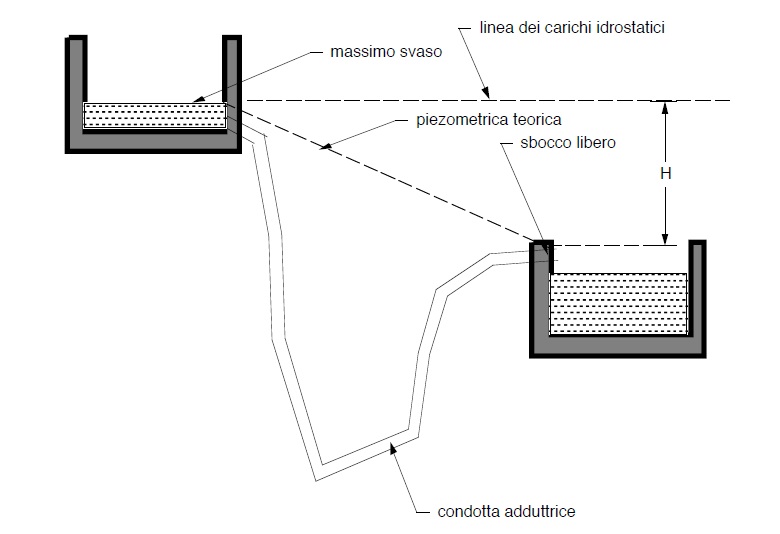
Spesso il serbatoio di monte é la vasca di carico di un’ opera di captazione. I calcoli idraulici, é ovvio, vanno fatti, per tener conto della minima cadente, in condizioni di massimo svaso del serbatoio a monte mentre, in genere, in quello a valle l’acqua sgorga liberamente.
Sia Q la portata da trasportare; è evidente che l ‘utilizzo di una qualsiasi delle formule precedenti, ad esempio la (59) da immediatamente il diametro da adottare, infatti:
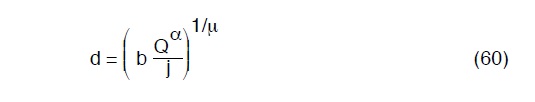
Ovviamente questo calcolo, come la maggior parte dei successivi porta a diametri non commerciali.
Sono possibili allora due scelte:
- o assegnare alla condotta due diametri, attribuendo ad un tronco il diametro d1 di commercio immediatamente inferiore al valore d fornito dalla (60) e all ‘ altro quello d2 immediatamente superiore,
dosando opportunamente le lunghezze L1 e L2; - oppure assegnare alla condotta il diametro commerciale immediatamente maggiore di quello di calcolo dato dalla (60). In tal caso si trasporterà una portata maggiore. Ma operando in modo da introdurre perdite di carico localizzate (per esempio tramite la strozzatura di una saracinesca o tramite una turbina posta all’ estremità della condotta2, cioé a monte del serbatoio di arrivo) si può comunque trasportate solo la portata desiderata.
Nel primo caso sono da determinare le lunghezze L1e L2 dei due tronchi a diverso diametro.
Indichiamo con J1e J2 le pendenze piezometriche corrispondenti ai diametri d1 e d2ottenuti tramite la(59):
Detto H il carico disponibile dovrà essere:

nonché, detta L la lunghezza totale della condotta:

2 L’introduzione di tali turbine ha senso solo per portate e salti considerevoli, ma ha il vantaggio di poter produrre energia.
Pertanto un sistema lineare di due equazioni nelle due incognite L1 e L2 , che risolto da:
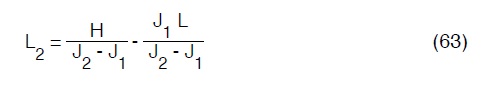
A seconda del tracciato altimetrico della condotta si collocherà prima il tronco di pendenza J2 e poi quello di perndenza J 1 o viceversa in modo che non risultino carichi piezometrici eccessivi (quindi spessore e costo eccessi della tubazione ) nè troppo ridotti, cioè inferiori o prossimi alla pressione atmosferica.
Risoluzione grafica del problema precedente
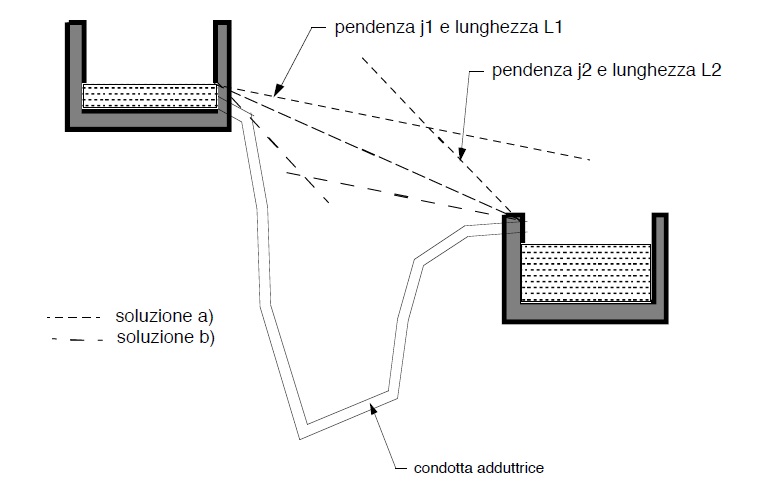
Condotta in materiali diversi senza erogazione lungo il percorso.congiungente due serbatoi
Più interessante è quando la stessa condotta precedente (cioè a portata costante ) debba essere costruita con materiali di diverso costo unitario.
Ciò può accadere se la condotta deve attraversare una depressione C tanto profonda da imporre o consigliare l ‘uso di materiale con caratteristiche resistenti migliori.
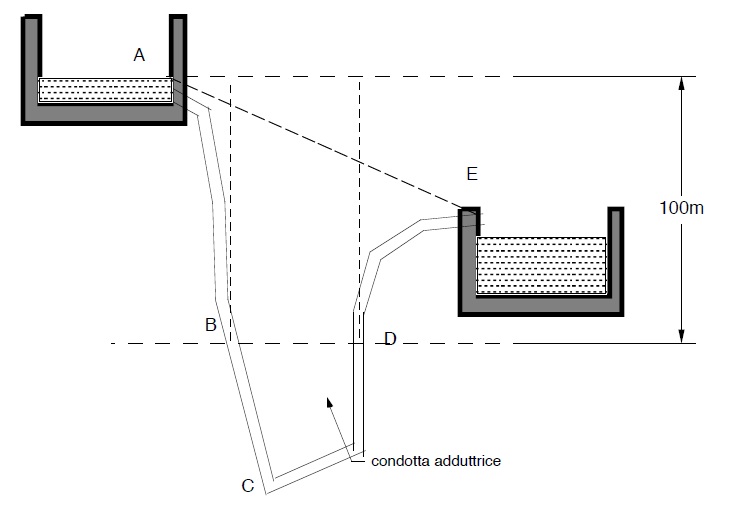
Con riferimento alla figura precedente i tratti AD e EB potrebbero essere realizzati ad esempio in P.R.F.V.in quanto i tubi dovranno resistere a pressioni al più di 10 atm (di fatto qialcosa in più tenuto conto del colpo d’ariete, all’uopo potremmo utiulizzare PRFV con PN 16) ed il tratto DE in acciaio.
In tal caso non esiste, come per il caso precedente, l ‘unicità della soluzione per il diametro per ciascun tratto, per convincersi di ciò basta osservare la fig. 26 dove con linea a tratto e punto è indicata una soluzione e con tratteggio semplice ne è indicata una differente.

La scelta dei diametri, in generale tre, uno per il tratto AD, uno per il tratto DE e l ‘altro per il tratto EB può essere effettuata secondo il criterio detto della massima economia cioé il costo della condotta deve essere il minimo. Da un punto di vista matematico il criterio si traduce nella
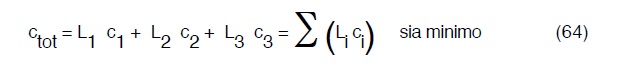
dove:
ci è il costo di un tratto di condotta di lunghezza unitaria;
Li è la lunghezza del tratto.
La (64) è soggetta al vincolo seguente:

ovviamente la (64) e la (65) qui scritte per 3 tronchi possono essere estese a qualsivoglia tronchi.
Il problema così posto é di minimo condizionamento che notoriamente può essere affrontato col ben noto metodo dei moltiplicatori di Lagrange, quindi é ricondotto alla ricerca del minimo della funzione
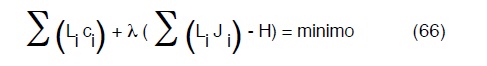
tale minimo va ricercato in funzione dei diametri d1, d2, d3 o, che é lo stesso, data la (60), in funzione di J1, J2, J3.
Segue dunque che potranno scriversi tante equazioni del tipo:
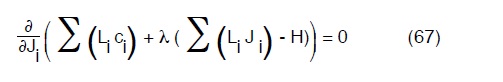
quanti i tronchi della condotta con caratteristiche diverse. Eseguendo la derivazione per il generico Ji avremo:

da cui l’ovvia conseguenza che tra due tronchi contigui l’i-esimo e l’i+1-esimo dovrà essre verificata la:

che è la condizione di economia ed il moltiplicatore di Lagrange λ costituisce quindi un’ invariante.
Ancorché oggi le costruzioni grafiche siano demodé, si ritiene tuttavia opportuno, e non solo per ragioni storiche, dare un cenno alla risoluzione grafica anche perché sono comunque utili per l’impostazione dei problemi sui fogli elettronici (EXCEL, LOTUS, che oggi costituiscono, per l’Idraulico gli strumenti attuali).
In un diagramma cartesiano si riportano in ascisse le pendenze J ed in ordinate i costi per unità di lunghezza e si tracciano le curve relative ai vari tipi di tubazione rappresentanti la funzione. La seguente tabella EXCEL riporta i calcoli relativi.
| Portata | Q= | 0,15 | [m^ 3 / s ] | |
| ø | costi | costi | Piezometria | Piezometria |
| [mm] | acciaio-BIRP | PRFV | acciaio-BIRP | PRFV |
| 300 | 80,468 | 57,266 | 1,76E-02 | 9,42E-03 |
| 400 | 116,639 | 93,260 | 4,17E-03 | 2,11E-03 |
| 500 | 155,560 | 136,138 | 1,37E-03 | 6,62E-04 |
| 600 | 196,822 | 185,441 | 5,50E-04 | 2,56E-04 |
| 700 | 240,138 | 240,821 | 2,54E-04 | 1,15E-04 |
| 800 | 285,295 | 301,997 | 1,30E-04 | 5,74E-05 |
| 900 | 332,125 | 368,737 | 7,24E-05 | 3,11E-05 |
| 1000 | 380.493 | 440,844 | 4,28E-05 | 1,80E-05 |
Un tale diagramma é quello qui di seguito rappresentato.
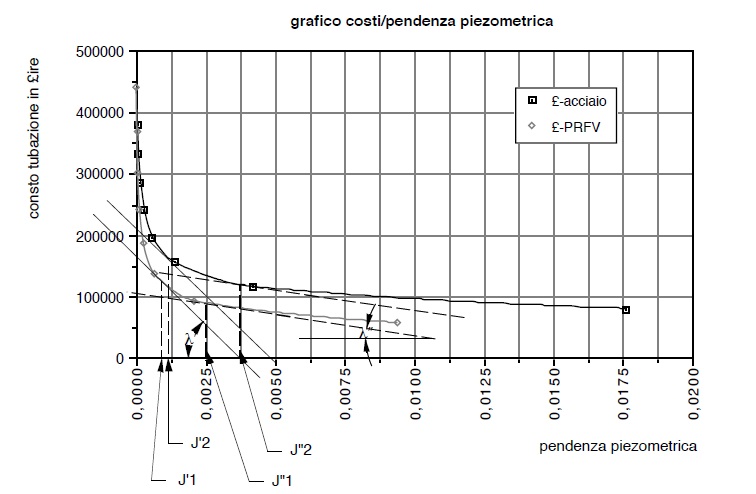
E’ necessario un breve commento.
Come é ovvio la soluzione economica é data dal sistema costituito dalle(68) e dalla (65).
Si fissa un valore di λ′ di primo tentativo e si individuana le due pendenze piezometriche J’1 e J’2
Conseguentemente si introducono tali valori nella (65),ma essendo i valori di J’1 e J’2 derivanti da un tentativo di norma avremo:
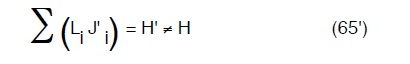
Si fissa un valore di λ″ di ulteriore tentativo e si individuano le due pendenze piezometriche J”1 e J”2 che introdotti nella (65) porteranno ad una:
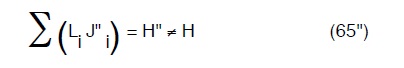
Sarebbe opportuno che H’ ed H” fossero l’uno maggiore e l’altro minore di H (o viceversa) ma trattasi sono di un’ opportunità. Si realizza a tal punto una nuova e banale costruzioni grafica, che altro non é che un’interpolazione (nella fattispecie lineare3)
3 Di fatto l’interpolazione non dovrebbe essere lineare ma stante il fatto che poi comunque occorrerà adottare diametri commerciali ed altre incertezze, l’interpolazione lineare é più che soddisfacente.
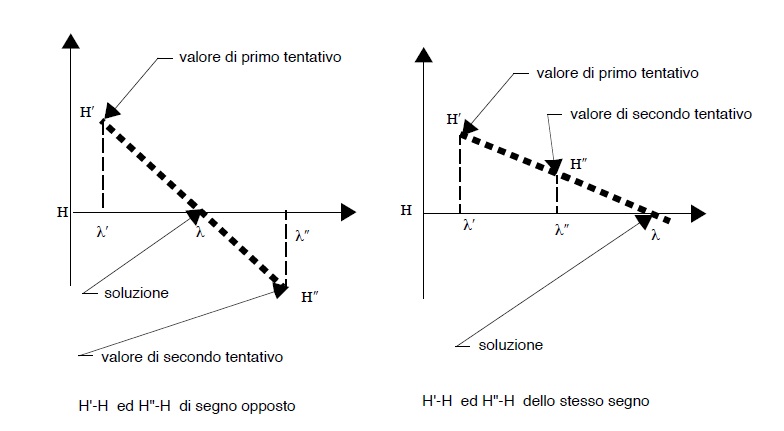
I ndividuato il valore di λ si tracciano le tangenti alle curve del precedentediagramma e si ottengoni i valori di J1 e J2che soddisfano la (65).
Condotta adduttrice che in alcuni punti del suo percorso eroghi
acqua tramite diramazioni.
Si tratta delle cosiddette condotte adduttrici consortili che possono essere schematizzate come in figura.
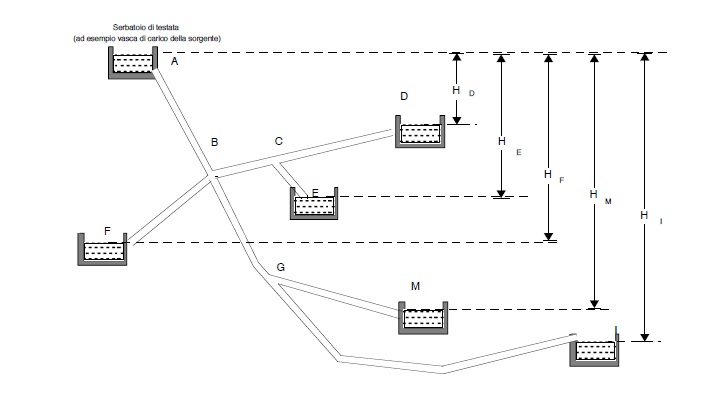
L’ acqua da un serbatoio di testata viene addotta con una condotta ad albero ai serbatoi D, E, F, M, I.
La condotta presenta nodi di estremità quali A, D, E, F, M, I e nodi intermedi o di diramazione.
Prima di affrontare i problemi di dimensionamento idraulico, peraltro trattasi di una semplice estensione del caso in precedenza esaminato , si ritiene opportuno un cenno alla teoria dei grafi4: trattasi di una estremamente interessante
4 I fondamenti della teoria dei grafi si devono a Leonardo Eulero che li applicò per la primavolta nel 1736. Altre applicazioni del passato sono dovute a Kirchoff (1847) per le reti elettriche, a Cayley (1857) per la chimica degli idrocarburi ed a De Morgan (1852).
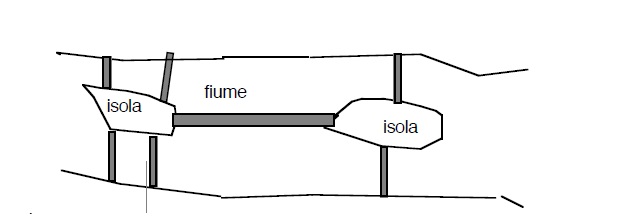
Eulero applicòla teoria dei grafi per risolvere il seguente problema:”é possibile per un pedone percorrere tutti i ponti di Koenisberg attraversandoli una volta sola ?” Il sistema dei ponti era il seguente
ed utile interpretazione topologica che seppur di concezione non certo recente, ha trovato largo uso con lo sviluppo dell’ algebra matriciale ed in particolare dell’ algebra booleana e dei computer.
Una qualunque struttura ad albero anche se chiusa ma comunque costituita da aste (nell’ ingegneria civile per esempio le travi, le condotte idriche o fognarie, il percorso di un autobus ecc….) e da nodi può essere riguardato come un grafo e la sua geometria può essere definita tramite una apposita matrice (matrice di incidenza) Se il verso di percorrenza delle aste é indifferente parleremo di grafi on orientati (e le relativi matrici di incidenza possono chiamarsi anche matrici booleane), altrimenti avremo grafi orientati, come nel caso degli acquedotti, delle fogne ecc…
Si definisce matrice topologica (o matrice di incidenza di un grafo orientato) una matrice A di generico elemento a i,j , dove l’indice di riga i é riferito ai nodi e l’indige di colonna j é riferito alle aste. Il generico elemento di una matrice di incidenza di un grafo orientato può assumere uno dei seguente tre valori.
1 se l’asta j converge nel nodo i (cioé, per gli acquedotti, se l’acqua in viaggia verso i);
-1 se l’asta j diverge nel nodo i (cioé se l’acqua in j si allontana da i);
0 se tra l’asta j ed il nodo i non esiste collegamento alcuno;
Con riferimento all’ esempio della figura precedente e dopo aver dato una numerazione (diversa) sia alle aste che ai nodi la matrice A
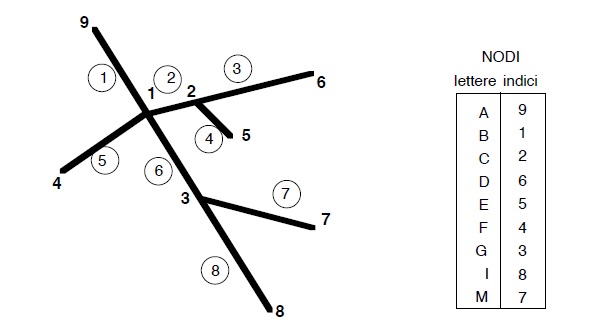
varrà dunque.
| Indice | ||||||||
| Asta | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Nodo | ||||||||
| 1 | 1 | -1 | 0 | 0 | -1 | -1 | 0 | 0 |
| 2 | 0 | 1 | -1 | -1 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 9 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
9
Trattasi dunque di una matrice molto sparsa (con parecchi elementi nulli) dove in ciascuna colonna vi sono al più soli elementi diversi non nulli (un lato non può avere che i due collegamenti alle estremità).
Nella tabella precedente si é sovrapposta realativamente ai nodi terminali un apposito retino a significare che la matrice può essere considerata partita in due, quindi possiamo sostituire alla unica A di prima una matrice del tipo
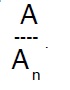
In quest’ ottica possiamo scrivere le equazioni di moto, cioé le analoghe delle (65) in maniera estremamente sintetica ed interessante.
Dette
qj le portate transitanti nel generico lato e q il relativo vettore riga;
Jj le pendenze piezometriche che si realizzano nei lati j e J il relativo vettore riga;
hj le perdite di carico che si realizzano nei lati j e h il relativo vettore riga;
AT la trasposta della parte superiore della A
AnT a trasposta della parte inferiore della A
H le piezometriche incognite dei nodi intermedi
Hn le piezometriche note dei nodi di estremità
Q il vettore colonna le portate direttamente fuoriscenti dai nodi intermedi (nel nostro caso tutte nulle)
Qn il vettore colonna le portate fuoriscenti dai nodi intermedi estremi, cioé qualle versate nei serbatoi.
ovviamente avremo:
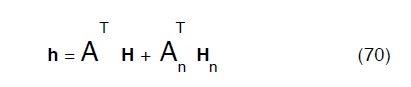
Parallelamente l’equazione di continuità (ai nodi) sarà data dalla:
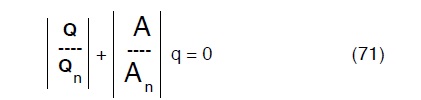
E’ evidente che le (70) e le (71) inquadrano completamente il problemaidraulico. Problema che peò come nel caso precedentemente non ha unica soluzione. Pertanto per dimensionare il sistema di condotte é necessario ricorrere anche il questo caso ad affiancare alle equazioni del sistema fisico delle condizioni
di economia, che ovviamente ora possono esprimersi con la
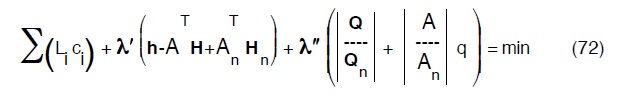
Con λ′ e λ′ matrici, la prima riga, l’altra colonna contenente tanti operatori di Laplace rispettivamente quante le righe e le colonne della matrice A Eseguendo la derivazione per il generico Ji ed ponendola eguale a zero, avremo:

Dove la sommatoria a secondo membro é estesa a tutti i lati che hano connessione con il lato i-esimo.
Ne segue dunque che assunto un verso, per esempio positivo nel senso del moto e negativo nel caso contrario alle
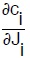
dovrà in generale essere:

Ovviamente la ((74) sarà valida anchez nel caso di condotte di diramazioni estremamente conte cioé con erogazioni concentrate lungo il percorso. Infatti nella conqizione di economia(73) non compaiono imoltiplicatori di Langange del tipo λ′ che sono relativi alla equazione di continuità che quindi non gioca a lcun ruolo sulla soluzione economica.
Il sistema, sempre in senso tradizionale, cioè senza ricorrere all’ uso di calcolatori elettronici, può essere risolto per tentativi, come visto in precedenza per tentativi
Adduttrici con distribuzione lungo il percorso
Nel caso di adduttrici con distribuzione lungo il percorso non vengono di norma esaminate questioni di economia in quanto una tale soluzione è di per se “fuori schema” . Si faccia riferimento alla figura seguente.
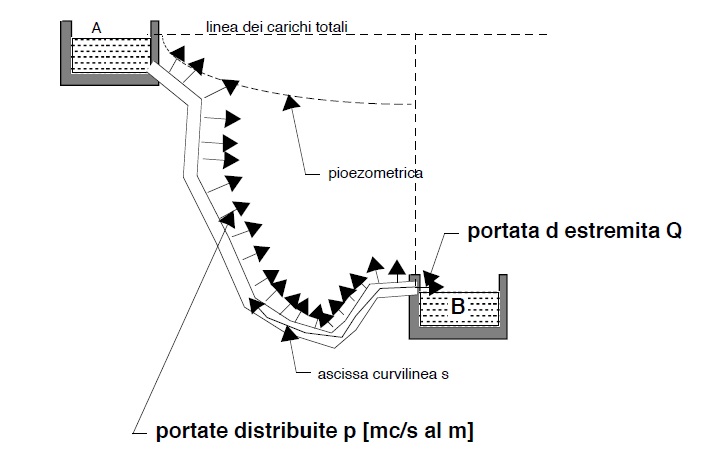
Ricordiamo qui tuttavia la procedura di verifica, già, nota, del resto, dall’ Idraulica.
Con riferimento alla figura seguente, detta:
Y la differenza di carico piezometrico tra i due serbatoi A e B
p la portata erogata per unità di percorso di tubazione,
s l ‘ascissa curvilinea lungo la tubazione a partire da B stessa
Q la portata da trasportare dal serbatoio A a B avremo che la portata alla generica assisa s sarà data dalla :

e la perdita di carico locale alla ascissa s sarà:
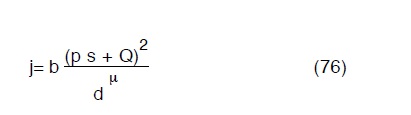
segue che:
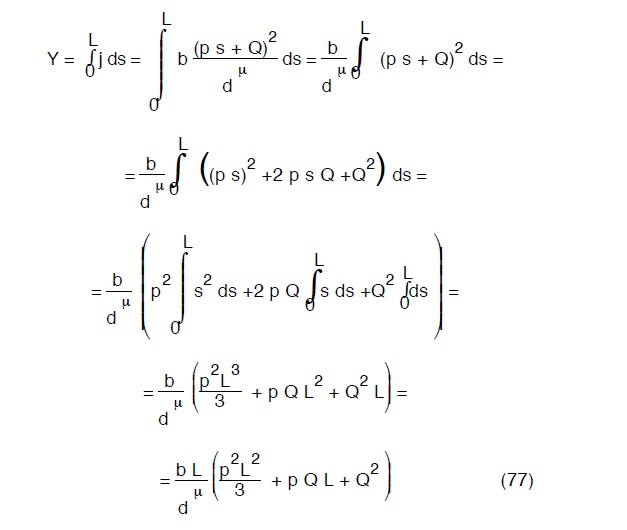
Si ponga ora P = p L cioé pari all’ intera portata distribuita lungo il percorso, la (77) diviene:
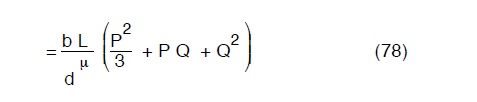
Il trinomio entro parentesi può essere sostituito con buona approssimazione con in quadrato del seguente binomio5:
5 svolgendo i calcoli avremo:
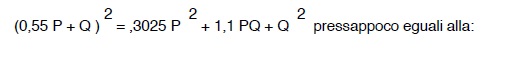
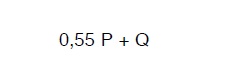
pertanto la (78) diventa:
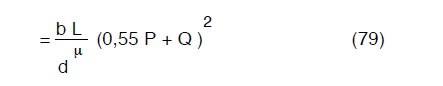
cioè un’ espressione formalmente analoga alla (45) pertanto si può asserire che una condotta che distribuisce lungo il percorso ha perdite di carico globali corrispondenti a quelle che avrebbe se trasportasse senza distribuire lungo il percorso una portata pari a quella di estremità aumentata di 0,55 volte la portata globalmente distribuita lungo il percorso.
Se Q = 0 , cioé se é nulla la portata di estremità la perdita di carico é esattamente 1/3 di quella corrispondente all’ intera portata distribuita, ma trasportata sino all’ estremità.
Per conoscere l’andamento intermedio (cioé lungo il percorso) della piezometrica occorre ricalcolare il precedente integrale (77) dall’ estremità s=0 all’ ascissa generica s, quindi
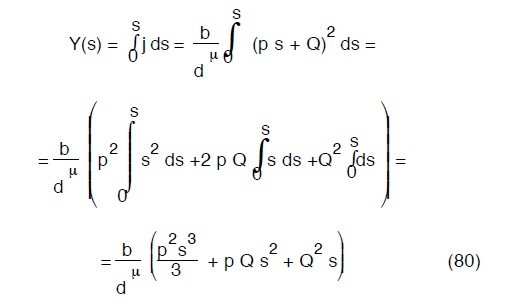
la linea piezometrica è dunque una parabola cubica.
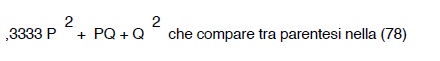
Se Q= 0 , cioé se manca il servizio di estremità la (80) si semplifica nella:

Condotte con sollevamento meccanico
Esaminiamo ora il caso, frequente, di condotta adduttrice con sollevamento meccanico, del tipo di quella illustrata nella figura seguente. In questi casi vi è un interessante problema di economia:
Converrà realizzare condotte piccole (e quindi contenere le spese di impianto) e poi avere maggiori perdite di carico (e quindi spendere cifre considerevoli per la energia necessaria al sollevamento), o viceversa?
Sia H il dislivello geodetico da superare ed Y la resistenza da vincere, notoriamente pari a J L (con L lunghezza della condotta e J perdita di carico distribuita).
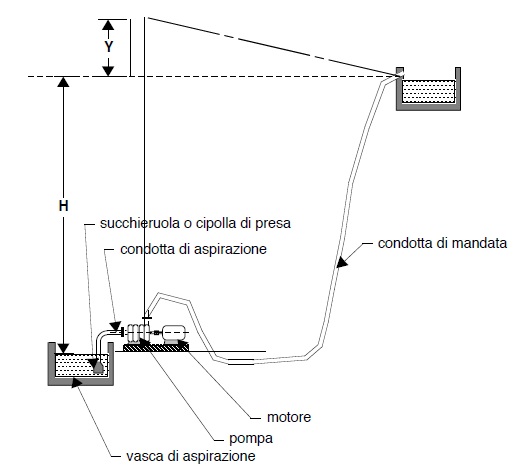
Il sollevamento della portata Q all’ altezza H+Y richiederà una potenza di:
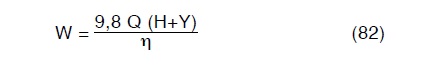
espressa in Kw, con η rendimento della stazione di spinta.
Pertanto l ‘ energia necessaria sarà:

essendo T le ore di funzionamento.
A tale energia corrisponde un costo Cf di funzionamento pari a:

con cKwh il costo, per acquedotti6, di 1 Kwh di energia.
D ‘altra parte il costo della condotta Cc sarà dato dalla:

Tenuto presente che gli acquedotti hanno una vita “tecnico economica” massima di 40÷50 anni la la quota annua di ammortamento del costo sarà data dalla:

dove r è un’ aliquota che rappresenta, a seconda che l’Ente acquedottistico finanzi l’opera tramite un mutuo da contrarre, ad esempio con la Cassa Depositi e Prestiti, o tramite l’utilizzzo di somme precedentemente accantonate,
rispettivamente:
a) l a rata annuale posticipata necessaria ad estinguere, in n anni, il debito di una lira. In questo caso il valore di r va valutato con la

b) la rata annuale anticipata necessaria ad estinguere, in n anni, il debito di una lira. In questo caso il valore di r va valutato con la
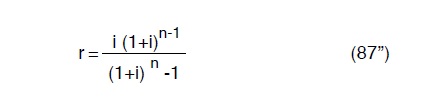
6 Il costo dell’ energia elettrica é differente a seconda degli usi, delle fasce orarie e del tipo di corrente che si adopera. Per gli acquedotti, in generale non é possibile utilizzare le fasce orarie economicamente
più convenienti cioé le notturne (occorerebbero dei serbatoi grandi) però se la centrale di sollevamento non é di piccolissima potenza é in generale conveniente apprivvigionare l’energia elettrica (trifase) non a bassa tensione (220 od a 380 Volt) ma in media tensione (M.T.) realizzando in proprio la trasformazione. In tal caso il costo del Kwh é minore.
c) la somma annua posticipata da accantonare necessaria a costituire in n anni, il capitale di una lira. In questo caso il valore di r va valutato con la

d) la somma annua anticipata da accantonare necessaria a costituire in n anni, il capitale di una lira. In questo caso il valore di r va valutato con la

Dove i é il tasso d’interesse richiesto dall’ istituto di credito (o corrisposto nel caso di accantonamento, sulle somme depositate) E ‘ da rilevare che date le varie incertezze di progettazione irrilevante l’uso della (87’) o della (87”) e della (88’) o (88”) cioè se le quote o le rate siano anticipate o posticipate (cioè versate od accantonate all ‘ inizio o alla fine di ciascun anno finanziario ). Si rileva ancora che il più delle volte la forma di finanziamento cui gli Enti acquedottistici fanno ricorso è quella del mutuo ed in tal caso è lecito per una vita economica dell’ ordine sopra indicato, semplificare le (87) nella

Dalle tabelle che seguono é evidente l’asserto.
| n= | 20 | ||||||||||
| i | 5% | 6% | 7% | 8% | 9% | 10% | 12% | 14% | 16% | 18% | 20% |
| r | 8,02% | 8,72% | 9,44% | 10,19% | 10,95% | 11,75% | 13,39% | 15,10% | 16,87% | 18,68% | 20,54% |
| n= | 30 | ||||||||||
| i | 5% | 6% | 7% | 8% | 9% | 10% | 12% | 14% | 16% | 18% | 20% |
| r | 6,51% | 7,26% | 8,06% | 8,88% | 9,73% | 10,61% | 12,41% | 14,28% | 16,19% | 18,13 | 20,08 |
| n= | 40 | ||||||||||
| i | 5% | 6% | 7% | 8% | 9% | 10% | 12% | 14% | 16% | 18% | 20% |
| r | 5,83% | 6,65% | 7,50% | 8,39% | 9,30% | 10,23% | 12,13% | 14,07% | 16,04% | 18,02% | 20,01% |
Ciò premesso il costo da minimizzare sarà dunque dato dalla:
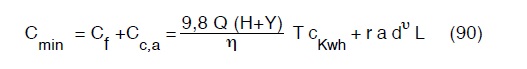
Si sostituisca nella precedente ad Y l’espressione della perdita di carico secondo Darcy-Contessini, avremo:
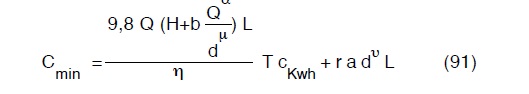
Eseguendo la derivata rispetto a d ed eguagliandola a zero avremo:
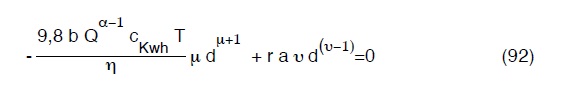
che esplicitata in d, risolve il problema postoci.
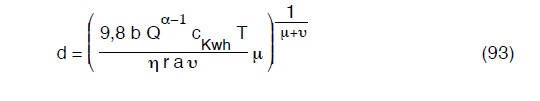
Impianto di sollevamento con diramazioni
E’ frequente sebbene non del tutto accettabile il caso che acqua captata da vari pozzi venga spinta da pompe sommerse dapprima in condotte singole che poi si riuniscono in un’ unica condotta che le convogli al serbatoio Io schema sarà quello della figura seguente
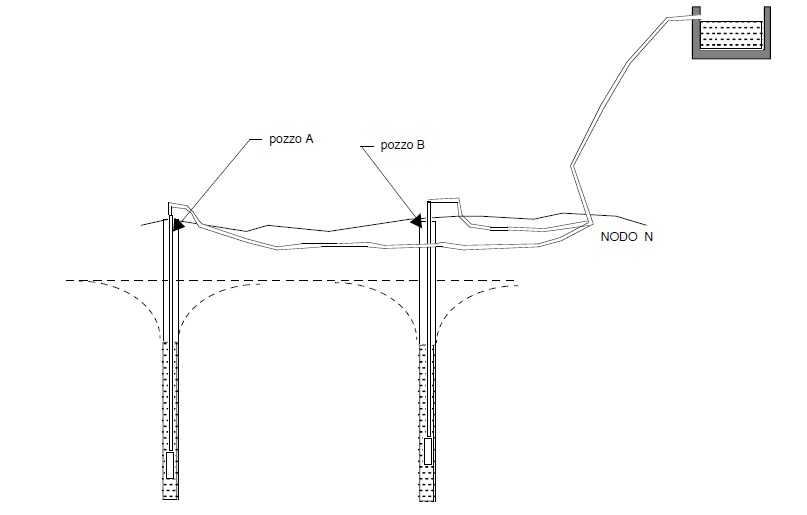
Anche in questo caso si pone un problema di minimo del tutto analogo a quello visto in precedenza .
Il costo del sollevamento sarà ora dato dalla:
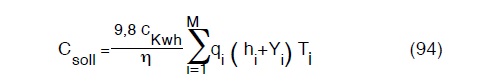
dove:
qi è la portata dell’ i-esimo pozzo
hi+Yi è il dislivello dal quale viene sollevata l’ acqua dall ‘ i-esimo pozzo
Ti sono le ore di funzionamento dell ‘ i-esimo pozzo .
Il costo delle condotte ricondotte a quote annuale è per quanto già visto, dato dalla:
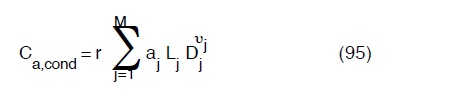
dove:
aj i coefficienti della (40) per il j-esimo tratto
υj gli esponenti della (40) per il j-esimo tratto
Lj le lunghezze del j-esimo tratto
e
Dj i diametri del j-esimo tratto.
Quindi la quantità da minimizzare sarà, il costo totale annuo espresso dalla:
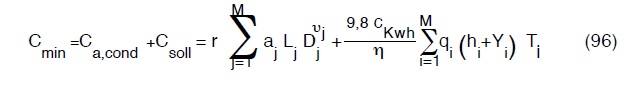
Se eseguiamo ora il bilancio incognite equazioni constatiamo che le prime sono in numero di N cioè gli N diametri dei vari tratti per ciascuno dei quali varrà la:
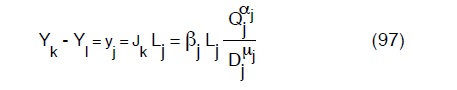
dove k ed l sono i nodi a monte ed a valle di ciascun lato j più le Yk e le Yl le quote piezometriche dei detti nodi
Si perviene al pareggio aggiungendo alle N equazioni (97) le M, equazioni di economia che si ottengono dalle (96) eguagliandone a zero p le derivate rispetto alla generica piezometrica Yl
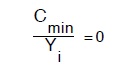
Tenuto conto che dalla (97) possiamo esplicitare la D come segue:
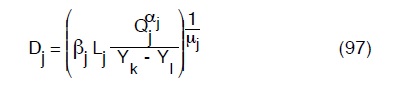
e che dunque la (96) diventa
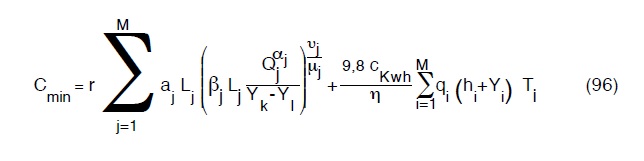
Per il generico pozzo avremo:
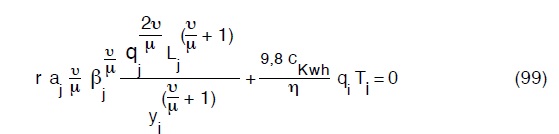
ripetendo tale operazione per i vari indici j e sostituendo alla fine avremo la soluzione del problema
